Cho hình chóp $S.ABCD$ . Gọi $M,N$ là hai điểm lần lượt thuộc cạnh $AB$ và \(CD;\left( \alpha \right)\) là mặt phẳng đi qua $MN$ và song song với $SA$ . Tìm điều kiện của $MN$ để thiết diện của hình chóp khi cắt bởi mp\(\left( \alpha \right)\) là một hình thang.
Trả lời bởi giáo viên
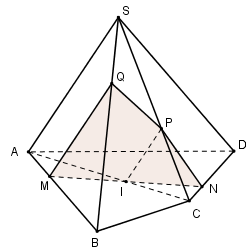
Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {SAB} \right)\\\left( \alpha \right)\parallel SA\\SA \subset \left( {SAB} \right)\end{array} \right. \Rightarrow \left( {SAB} \right) \cap \left( \alpha \right) = MQ\parallel SA\,\,\left( {Q \in SB} \right).\)
Trong (ABCD), gọi \(I = MN \cap AC\). Ta có:
\(\begin{array}{l}I \in MN,\,MN \subset \left( \alpha \right) \Rightarrow I \in \left( \alpha \right).\\I \in AC,\,AC \subset \left( {SAC} \right) \Rightarrow T \in \left( {SAC} \right)\\ \Rightarrow I \in \left( \alpha \right) \cap \left( {SAC} \right).\end{array}\)
Vậy \(\left\{ \begin{array}{l}I \in \left( \alpha \right) \cap \left( {SAC} \right)\\\left( \alpha \right)\parallel SA\\SA \subset \left( {SAC} \right)\end{array} \right. \Rightarrow \left( {SAC} \right) \cap \left( \alpha \right) = IP\parallel SA\,\,\left( {P \in SC} \right).\)
Thiết diện là tứ giác $MNPQ$ .
Để tứ giác $MNPQ$ là hình thang thì cần $MQ//NP$ hoặc $MN//PQ$ .
Trường hợp 1: Nếu $MQ//NP$ thì
Ta có: \(\left\{ \begin{array}{l}MQ\parallel NP\\MQ\parallel SA\end{array} \right. \Rightarrow SA\parallel NP,\) mà \(NP \subset \left( {SCD} \right) \Rightarrow SA\parallel \left( {SCD} \right)\) (Vô lí).
Trường hợp 2: Nếu $MN//PQ$ thì ta có các mặt phẳng $\left( {ABCD} \right),\left( \alpha \right),\left( {SBC} \right)$ đôi một cắt nhau theo ba giao tuyến là $MN,BC,PQ$ nên $MN//BC$.
Đảo lại nếu $MN//BC$ thì \(\left\{ \begin{array}{l}PQ = \left( \alpha \right) \cap \left( {SBC} \right)\\MN \subset \left( \alpha \right)\\BC \subset \left( {SBC} \right)\end{array} \right. \Rightarrow PQ\parallel MN\parallel BC\) nên tứ giác $MNPQ$ là hình thang.
Vậy tứ giác $MNPQ$ là hình thang thì điều kiện là $MN//BC$ .
Hướng dẫn giải:
- Xác định thiết diện dựa vào yếu tố song song với $SA$.
- Để một tứ giác trở thành hình thang cần thêm điều kiện một cặp cạnh đối song song.
Giải thích thêm:
Khi dựng các đường thẳng quy một điểm $M$ và song song với đường thẳng $d$ cho trước rất nhiều học sinh dựng một cách “tùy tiện”, hoặc “mông lung” trong cách dựng hình. Để dựng được hình một cách chính xác các em cần dựng đường thẳng song song trong mặt phẳng chứa điểm $M$ và đường thẳng $d$

