Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = 2\) và \(AD = 1\). Gọi \(M\) là trung điểm của \(DC\). Biết \(SA \bot \left( {ABCD} \right)\) và \(SA = 2\) (tham khảo hình vẽ bên). Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.BCM\).

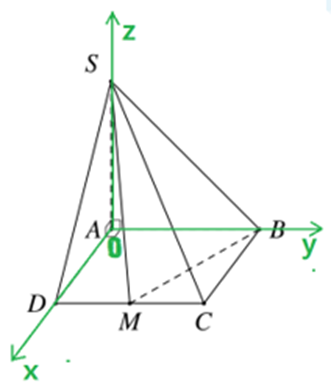
Gắn hệ trục tọa độ \(Oxyz\) như hình vẽ. Trong đó: \(S\left( {0;0;2} \right),\,B\left( {0;2;0} \right),\,D\left( {1;0;0} \right),\) \(C\left( {1;2;0} \right),\,M\left( {1;1;0} \right)\).

Gọi \(I\left( {a;b;c} \right)\) là tâm mặt cầu ngoại tiếp hình chóp \(S.BCM\). Ta có: \(IS = IB = IC = IM\).

Suy ra \(\left\{ \begin{array}{l}I{S^2} = I{B^2}\\I{S^2} = I{C^2}\\I{S^2} = I{M^2}\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} + {\left( {c - 2} \right)^2} = {a^2} + {\left( {b - 2} \right)^2} + {c^2}\\{a^2} + {b^2} + {\left( {c - 2} \right)^2} = {\left( {a - 1} \right)^2} + {\left( {b - 2} \right)^2} + {c^2}\\{a^2} + {b^2} + {\left( {c - 2} \right)^2} = {\left( {a - 1} \right)^2} + {\left( {b - 1} \right)^2} + {c^2}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l} - 4c + 4 =  - 4b + 4\\ - 4c + 4 =  - 2a + 1 - 4b + 4\\ - 4c + 4 =  - 2a + 1 - 2b + 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b - c = 0\\2a + 4b - 4c = 1\\2a + 2b - 4c =  - 2\end{array} \right. \)\( \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\\b = \dfrac{3}{2}\\c = \dfrac{3}{2}\end{array} \right.\,\,\,\,\, \Rightarrow I\left( {\dfrac{1}{2};\dfrac{3}{2};\dfrac{3}{2}} \right)\).

Vậy bán kính mặt cầu \(R = IS = \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + {{\left( {\dfrac{3}{2}} \right)}^2} + {{\left( { - \dfrac{1}{2}} \right)}^2}}  = \dfrac{{\sqrt {11} }}{2}\).