Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\), \(BC = a\), cạnh bên $SA$ vuông góc với đáy, \(SA = a\sqrt 3 \). Gọi \(M\) là trung điểm của \(AC\). Tính côtang góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\).
Trả lời bởi giáo viên
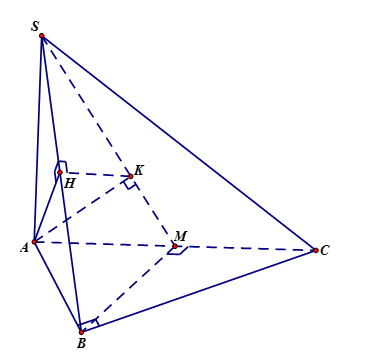
Kẻ \(AH \bot SB\) và \(AK \bot SM\).
Vì tam giác \(ABC\) vuông cân tại \(B\)và \(BC = a\)cùng với $SA \bot \left( {ABC} \right)$ nên suy ra \(BM \bot \left( {SAC} \right)\) và \(BM = AM = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}\). Do đó \(BM \bot AK\).
Từ \(BM \bot AK\) và \(AK \bot SM\) suy ra \(AK \bot \left( {SBM} \right)\)\( \Rightarrow AK \bot SB\).
Từ \(AH \bot SB\) và \(AK \bot SB\) ta có \(\left( {AHK} \right) \bot SB\). Do đó, góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\) bằng hoặc bù với góc \(\widehat {AHK}\).
Ta có:
$AH = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }}$$ = \dfrac{{a.a\sqrt 3 }}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {a^2}} }}$$ = \dfrac{{a\sqrt 3 }}{2}$.
$AK = \dfrac{{SA.AM}}{{\sqrt {S{A^2} + A{M^2}} }}$$ = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a\sqrt 3 }}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} }}$$ = \dfrac{{a\sqrt {21} }}{7}$.
Từ \(\left( {AHK} \right) \bot SB\) ta có \(HK \bot SB\) nên \(\Delta SHK \sim \Delta SMB\), do đó \(\dfrac{{HK}}{{MB}} = \dfrac{{SK}}{{SB}}\).
Mặt khác
\(SK.SM = S{A^2}\)\( \Rightarrow SK = \dfrac{{S{A^2}}}{{SM}}\)\( = \dfrac{{{{\left( {a\sqrt 3 } \right)}^2}}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} }}\)\( = \dfrac{{3a\sqrt {14} }}{7}\);
\(SB = \sqrt {S{A^2} + A{B^2}} = 2a\);
Nên \(\dfrac{{HK}}{{MB}} = \dfrac{{SK}}{{SB}} = \dfrac{{3\sqrt {14} }}{{14}}\)\( \Rightarrow HK = \dfrac{{3\sqrt {14} }}{{14}}.MB\)\( = \dfrac{{3\sqrt {14} }}{{14}}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{3a\sqrt 7 }}{{14}}\).
Trong tam giác \(AHK\) ta có:
\(\cos \widehat {AHK} = \dfrac{{A{H^2} + H{K^2} - A{K^2}}}{{2.AH.HK}}\)\( = \dfrac{{{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\dfrac{{3a\sqrt 7 }}{{14}}} \right)}^2} - {{\left( {\dfrac{{a\sqrt {21} }}{7}} \right)}^2}}}{{2.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{3a\sqrt 7 }}{{14}}}}\)\( = \dfrac{{\sqrt {21} }}{7}\).
Như vậy, góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\)là \(\alpha \) với \(\cos \alpha = \dfrac{{\sqrt {21} }}{7}\)\( \Rightarrow \sin \alpha = \dfrac{{2\sqrt 7 }}{7}\). Bởi vậy: \(\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }} = \dfrac{{\sqrt 3 }}{2}\).
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng \(\left( {SBM} \right)\) và \(\left( {SAB} \right)\), sử dụng lý thuyết: Góc giữa hai mặt phẳng (không vuông) là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng mà vuông góc với giao tuyến.
- Tính cô tang góc vừa xác định, sử dụng kiến thức hình học đã biết.

