Câu hỏi:
3 năm trước
Cho tứ diện $ABCD$ đều cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $BCD$. Góc giữa $AO$ và $CD$ bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: c
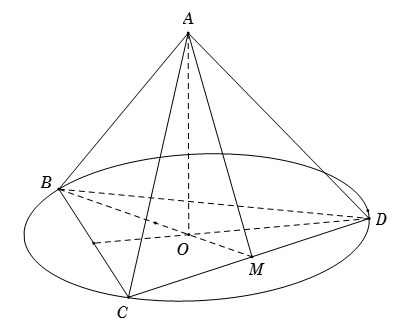
Gọi \(M\) là trung điểm của \(CD\).
Vì $ABCD$ là tứ diện đều nên \(AM \bot CD,\,\,OM \bot CD.\)
Ta có \(\overrightarrow {CD} .\overrightarrow {AO} = \overrightarrow {CD} .\left( {\overrightarrow {AM} + \overrightarrow {MO} } \right) = \overrightarrow {CD} .\overrightarrow {AM} + \overrightarrow {CD} .\overrightarrow {MO} = 0.\)
Suy ra \(\overrightarrow {AO} \bot \overrightarrow {CD} \) nên số đo góc giữa hai đường thẳng $AO$ và $CD$ bằng \({90^0}.\)
Hướng dẫn giải:
- Gọi \(M\) là trung điểm của \(CD\).
- Tính tích vô hướng của hai véc tơ \(\overrightarrow {AO} ,\overrightarrow {CD} \) rồi kết luận.

