Câu hỏi:
2 năm trước
Cho hình bình hành \(ABCD\). Trên đường chéo \(AC\) lấy điểm \(E\) sao cho \(AC = 3AE\). Qua \(E\) vẽ đường thẳng song song với \(CD\), cắt \(AD\) và \(BC\) theo thứ tự ở \(M\) và \(N\). Cho các khẳng định sau:
(I) \(\Delta AME\backsim\Delta ADC,\) tỉ số đồng dạng \(k{_1} = \dfrac{1}{3}.\)
(II) \(\Delta CBA\backsim\Delta ADC,\) tỉ số đồng dạng bằng \({k_2} = 1\).
(III) \(\Delta CNE\backsim\Delta ADC,\) tỉ số đồng dạng \({k_3} = \dfrac{2}{3}.\)
Số khẳng định đúng là:
Trả lời bởi giáo viên
Đáp án đúng: c
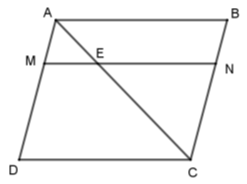
Vì \(ABCD\) là hình bình hành nên \(ME\) // \(DC\) và \(EN\) // \(AB\).
+ \(ME\) // \(DC\) nên \(\Delta AME\backsim\Delta ADC,\) tỉ số đồng dạng \(\dfrac{{AE}}{{AC}} = \dfrac{1}{3}.\)
+ Vì \(ABCD\) là hình bình hành nên \(\widehat B = \widehat D;\,AD = BC;\,AB = DC\) \( \Rightarrow \Delta CBA = \Delta ADC\) nên \(\Delta CBA\backsim\Delta ADC,\) tỉ số đồng dạng bằng \(1\) .
+ \(EN\) // \(AB\) nên \(\Delta CNE\backsim\Delta CBA,\) do đó \(\Delta CNE\backsim\Delta ADC,\) tỉ số đồng dạng \(\dfrac{{CE}}{{AC}} = \dfrac{2}{3}.\)
Vậy cả (I), (II), (III) đều đúng nên có \(3\) khẳng định đúng.
Hướng dẫn giải:
+ Sử dụng định lý về tam giác đồng dạng: Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Và tỉ lệ cạnh để suy ra tỉ số đồng dạng.
+ Sử dụng kiến thức: Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng là \(1\).
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
