Câu hỏi:
2 năm trước
Cho hình bình hành $ABCD,$ điểm $F$ nằm trên cạnh $BC.$ Tia $AF$ cắt $BD$ và $DC$ lần lượt ở $E$ và $G.$ Chọn câu đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: c
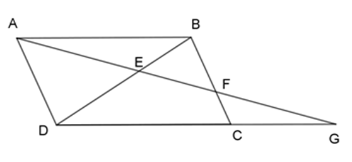
+) Vì $ABCD$ là hình bình hành nên \(AD//BC\)
\( \Rightarrow AD//BF\) (tính chất hbh).
Xét \(\Delta BEF\) và \(\Delta DEA\) có:
\(\widehat {BEF} = \widehat {DEA}\) (2 góc đối đỉnh)
\(\widehat {FBE} = \widehat {ADE}\) (cặp góc so le trong bằng nhau)
\( \Rightarrow \Delta BEF \backsim \Delta DEA\;(g - g)\) nên A sai.
+) Vì $ABCD$ là hình bình hành nên \(AB//DC\)
\( \Rightarrow AB//DG\)
Xét \(\Delta DGE\) và \(\Delta BAE\) ta có:
\(\widehat {DEG} = \widehat {BEA}\) (2 góc đối đỉnh)
\(\widehat {ABE} = \widehat {GDE}\) (cặp góc so le trong bằng nhau)
\( \Rightarrow \Delta DGE \backsim \Delta BAE\;(g - g)\) nên B sai.
+) Vì \(\Delta BEF \backsim \Delta DEA\) nên \(\dfrac{{EF}}{{EA}} = \dfrac{{BE}}{{DE}}\) (1)
Vì \(\Delta DGE \backsim \Delta BAE\) nên \(\dfrac{{AE}}{{GE}} = \dfrac{{BE}}{{DE}}\) (2)
Từ (1) và (2) ta có:
\(\dfrac{{EF}}{{EA}} = \dfrac{{AE}}{{GE}} \Leftrightarrow A{E^2} = GE.EF\) nên C đúng.
Hướng dẫn giải:
- Áp dụng cách chứng minh tam giác đồng dạng để chứng minh các cặp tam giác đồng dạng.
- Từ đó tìm ra tỉ lệ thức phù hợp để suy ra hệ thức đúng về cạnh.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
