Câu hỏi:
2 năm trước
Cho hình bình hành $ABCD$ có $AB = a, BC = b(a>b).$ Các phân giác trong của các góc $A, B, C, D$ tạo thành tứ giác $MNPQ.$
Tính độ dài đường chéo của hình chữ nhật$MNPQ$ theo \(a,\,b\) .
Trả lời bởi giáo viên
Đáp án đúng: b
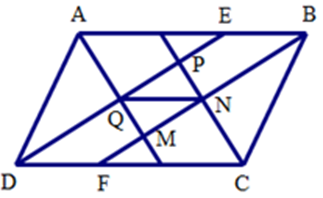
Gọi $E$ là giao điểm $PQ$ và $AB$ , $F$ là giao điểm của $MN$ và $CD$ . Tam giác $ADE$ có phân giác $AQ$ cũng là đường cao do đó tam giác cân tại $A$ , suy ra $DQ = QE = DE:2$ .
Tương tự tam giác $BCF$ cân tại$C$ , do đó $FN = BN = BF:2.$
Ta lại có $DEBF$ là hình bình hành (cặp cạnh đối song song), suy ra $DE = BF$ .
Suy ra $DQ = FN$ và $DQ$ //$FN$ . Vậy $DQNF$ là hình bình hành, từ đó $QN = DF = CD--CF$
Mà $CD = AB = a$ , $CF = CB = b$ , do đó: $QN = a-b$ .
Hướng dẫn giải:
Bước 1: Chứng minh $DQNF$ là hình bình hành dựa vào dấu hiệu tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành.
Bước 2: Tính độ dài đường chéo hình chữ nhật thông qua cạnh $DF$ của hình bình hành $DQNF$ (do$QN = DF$ ).
