Cho hàm số $y = {x^4} - 4{x^2} + 3$. Tìm tất cả các giá trị của tham số $m$ sao cho phương trình $\left| {{x^4} - 4{x^2} + 3} \right| = m$ có $4$ nghiệm phân biệt.
Trả lời bởi giáo viên
Số nghiệm của pt $\left| {{x^4} - 4{x^2} + 3} \right| = m$(*) số giao điểm của đồ thị hàm số $y = \left| {{x^4} - 4{x^2} + 3} \right|$ và đường thẳng $y = m$.
Ta có đồ thị hàm số $y = \left| {{x^4} - 4{x^2} + 3} \right|$ như hình vẽ:
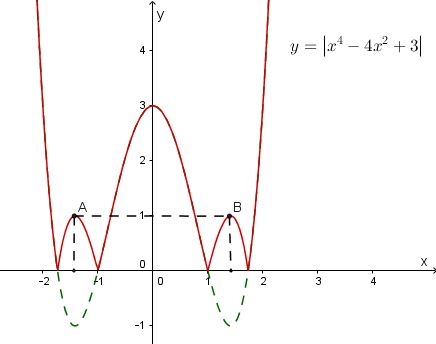
Để pt $(*)$ có $4$ nghiệm phân biệt thì đường thẳng $y = m$ cắt đồ thị hàm số $y = \left| {{x^4} - 4{x^2} + 3} \right|$ tại $4$ điểm phân biệt.
Quan sát đồ thị ta thấy đường thẳng cắt đồ thị hàm số $y = \left| {{x^4} - 4{x^2} + 3} \right|$ tại $4$ điểm phân biệt $ \Leftrightarrow \left[ \begin{gathered} m = 0 \hfill \\ 1 < m < 3 \hfill \\ \end{gathered} \right.$
Hướng dẫn giải:
- Vẽ đồ thị hàm số $y = \left| {f\left( x \right)} \right|$ từ đồ thị hàm số $y = f\left( x \right)$:
Trước hết ta vẽ đồ thị hàm số $y = f\left( x \right)$.
Ta có: $y = \left| {f\left( x \right)} \right| = \left\{ \begin{gathered} f\left( x \right)\,\,\,\,\,\,\,khi\,\,\,f\left( x \right) \geqslant 0 \hfill \\ - f\left( x \right)\,\,\,\,khi\,\,\,f\left( x \right) \leqslant 0 \hfill \\ \end{gathered} \right.$
Do đó đồ thị hàm số $y = \left| {f\left( x \right)} \right|$ gồm hai phần:
+) Phần 1: Giữ lại phần đồ thị hàm số $y = f\left( x \right)$ ở phía trên trục hoành.
+) Phần 2: Lấy đối xứng phần đồ thị hàm số $y = f\left( x \right)$ ở phía dưới trục hoành lên phía trên qua trục hoành sau đó xóa đi phần đồ thị phía dưới trục hoành
- Biện luận số nghiệm của phương trình dựa vào số giao điểm của đường thẳng và đường cong vừa vẽ được.

