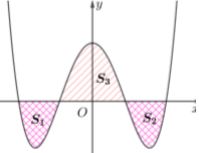
Cho hàm số \(y = {x^4} - 3{x^2} + m\) có đồ thị là \(\left( {{C_m}} \right)\) (\(m\) là tham số thực). Giả sử \(\left( {{C_m}} \right)\) cắt trục \(Ox\) tại 4 điểm phân biệt. Gọi \({S_1},\,\,{S_2}\) là diện tích của hai hình phẳng nằm dưới trục \(Ox\) và \({S_3}\) là diện tích của hình phẳng nằm trên trục \(Ox\) được tạo bởi \(\left( {{C_m}} \right)\) với trục \(Ox\). Biết rằng tồn tại duy nhất giá trị \(m = \dfrac{a}{b}\) (với \(a,\,\,b \in {\mathbb{N}^*}\) và tối giản) để \({S_1} + {S_2} = {S_3}\). Giá trị của \(2a - b\) bằng:

Xét phương trình hoành độ giao điểm: \({x^4} - 3{x^2} + m = 0\,\,\,\left( 1 \right)\).

Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\), khi đó phương trình (1) trở thành \({t^2} - 3t + m = 0\,\,\,\left( 2 \right)\).

Vì đồ thị hàm số \(y = {x^4} - 3{x^2} + m\) cắt trục hoành tại 4 điểm phân biệt nên phương trình (1) có 4 nghiệm phân biệt, do đó phương trình (2) phải có 2 nghiệm dương phân biệt.

\( \Rightarrow \left\{ \begin{array}{l}\Delta  > 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 - 4m > 0\\3 > 0\,\,\left( {luon\,\,dung} \right)\\m > 0\end{array} \right. \Leftrightarrow 0 < m < \dfrac{9}{4}\,\,\,\left( * \right)\).

Giả sử phương trình (2) có 2 nghiệm dương phân biệt \(0 < {t_1} < {t_2}\), áp dụng định lí Vi-ét ta có \(\left\{ \begin{array}{l}{t_1} + {t_2} = 3\\{t_1}{t_2} = m\end{array} \right.\). Khi đó phương trình (1) có 4 nghiệm phân biệt \( - \sqrt {{t_2}}  <  - \sqrt {{t_1}}  < \sqrt {{t_1}}  < \sqrt {{t_2}} \).

Do tính đối xứng qua trục tung của hàm đa thức bậc bốn trùng phương nên \({S_1} = {S_2}\), do đó theo bài ra ta có \({S_1} + {S_2} = {S_3} \Leftrightarrow 2{S_1} = {S_3}\).

Ta có:

\({S_2} = \int\limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } {\left| {f\left( x \right)} \right|dx}  =  - \int\limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } {f\left( x \right)dx} \)

\({S_3} = \int\limits_{ - \sqrt {{t_1}} }^{\sqrt {{t_1}} } {\left| {f\left( x \right)} \right|dx}  = \int\limits_{ - \sqrt {{t_1}} }^{\sqrt {{t_1}} } {f\left( x \right)dx}  = 2\int\limits_0^{\sqrt {{t_1}} } {f\left( x \right)dx} \)  (do \(f\left( x \right)\) là hàm chẵn).

Ta có:

\(\begin{array}{l}2{S_2} = {S_3}\\ \Leftrightarrow  - 2\int\limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } {f\left( x \right)dx}  = 2\int\limits_0^{\sqrt {{t_1}} } {f\left( x \right)dx} \\ \Leftrightarrow 2\left( {\int\limits_0^{\sqrt {{t_1}} } {f\left( x \right)dx}  + \int\limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } {f\left( x \right)dx} } \right) = 0\\ \Leftrightarrow 2\int\limits_0^{\sqrt {{t_2}} } {f\left( x \right)dx}  = 0 \Leftrightarrow \int\limits_0^{\sqrt {{t_2}} } {f\left( x \right)dx}  = 0\\ \Leftrightarrow \int\limits_0^{\sqrt {{t_2}} } {\left( {{x^4} - 3{x^2} + m} \right)dx}  = 0\\ \Leftrightarrow \left. {\left( {\dfrac{{{x^5}}}{5} - {x^3} + mx} \right)} \right|_0^{\sqrt {{t_2}} } = 0\\ \Leftrightarrow \dfrac{{{{\left( {\sqrt {{t_2}} } \right)}^5}}}{5} - {\left( {\sqrt {{t_2}} } \right)^3} + m\sqrt {{t_2}}  = 0\\ \Leftrightarrow \sqrt {{t_2}} \left( {\dfrac{{{t^2}}}{5} - t + m} \right) = 0\\ \Leftrightarrow \dfrac{{t_2^2}}{5} - {t_2} + m = 0\,\,\,\left( {Do\,\,{t_2} > 0} \right)\\ \Leftrightarrow t_2^2 - 5{t_2} + 5m = 0\,\,\left( * \right)\end{array}\)

Mà \({t_2}\) là nghiệm của phương trình \({t^2} - 3t + m = 0\) nên \(t_2^2 - 3{t_2} + m = 0\) và \({t_2} = \dfrac{{3 + \sqrt {9 - 4m} }}{2}\).

Do đó

\(\begin{array}{l}\left( * \right) \Leftrightarrow t_2^2 - 3{t_2} + m - 2{t_2} + 4m = 0\\ \Leftrightarrow  - 2{t_2} + 4m = 0 \Leftrightarrow {t_2} = 2m\end{array}\)

 \(\begin{array}{l} \Rightarrow \dfrac{{3 + \sqrt {9 - 4m} }}{2} = 2m\\ \Leftrightarrow 3 + \sqrt {9 - 4m}  = 4m\\ \Leftrightarrow \sqrt {9 - 4m}  = 4m - 3\\ \Leftrightarrow \left\{ \begin{array}{l}4m - 3 > 0\\9 - 4m = 16{m^2} - 24m + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{3}{4}\\16{m^2} - 20m = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{3}{4}\\\left[ \begin{array}{l}m = 0\\m = \dfrac{5}{4}\end{array} \right.\end{array} \right. \Leftrightarrow m = \dfrac{5}{4}\,\,\left( {tm\,\,*} \right)\end{array}\)

Vậy \(a = 5,\,\,b = 4 \Rightarrow 2a - b = 10 - 4 = 6.\)