Câu hỏi:
2 năm trước
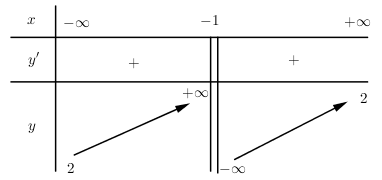
Cho hàm số y=x−2x+1 có đồ thị (C). Tiếp tuyến d của đồ thị (C) tạo với hai tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó khoảng cách từ I(−1;1) đến d bằng
Trả lời bởi giáo viên
Đáp án đúng: b
Phương trình tiếp tuyến tại điểm x = a là :
y=3(a+1)2(x−a)+a−2a+1 ( d )
Đường thẳng d cắt các tiệm cận tại : A(−1;a2−4a−5(a+1)2);B(2a+1;1)
Suy ra:
AI=|6a+1|;BI=|2a+2|=>AI.BI=12,∀a
Áp dụng công thức ở phần phương pháp ta có :
r=AI.BIAI+BI+√AI2+BI2≤122√AI.BI+√2AI.BI=√61+√2
Dấu bằng xảy ra khi AI=BI , suy ra tam giác ABI vuông cân , suy ra khoảng cách từ I tới d bằng √6
Hướng dẫn giải:
Sử dụng công thức
SABC=√p(p−a)(p−b)(p−c)=12r.(a+b+c)