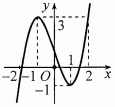
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( {\sqrt {4 - {x^2}} } \right) = m\) có nghiệm thuộc nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) là
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Bước 1: Tính \(\left[ {f\left( {\sqrt {4 - {x^2}} } \right)} \right]'\) và tìm nghiệm của \(\left[ {f\left( {\sqrt {4 - {x^2}} } \right)} \right]' = 0\).
Xét hàm \(y = f\left( {\sqrt {4 - {x^2}} } \right)\) trên nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) ta có:
\(y' = {\left[ {f\left( {\sqrt {4 - {x^2}} } \right)} \right]^\prime }\) \( = {\left( {\sqrt {4 - {x^2}} } \right)^\prime }.f'\left( {\sqrt {4 - {x^2}} } \right)\) \( = \dfrac{{ - x.f'\left( {\sqrt {4 - {x^2}} } \right)}}{{\sqrt {4 - {x^2}} }}\)
\(y' = 0 \Leftrightarrow x.f'\left( {\sqrt {4 - {x^2}} } \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{f'\left( {\sqrt {4 - {x^2}} } \right)}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{\sqrt {4 - {x^2}} {\rm{\;}} = {\rm{\;}} - 1}\\{\sqrt {4 - {x^2}} {\rm{\;}} = 1}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = {\rm{\;}} \pm \sqrt 3 {\rm{\;}} \notin \left[ { - \sqrt 2 ;\sqrt 3 } \right)}\end{array}} \right. \Leftrightarrow x = 0\)
Bước 2: Lập bảng biến thiên của hàm số \(y = f\left( {\sqrt {4 - {x^2}} } \right)\) trên nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) rồi suy ra tập giá trị của \(m\).
Bảng biến thiên:
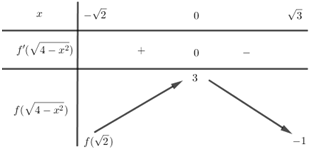
Từ đồ thị hàm số đã cho ta thấy \( - 1 < f\left( {\sqrt 2 } \right)\) nên để phương trình \(f\left( {\sqrt {4 - {x^2}} } \right) = m\) có nghiệm trong nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) thì \( - 1 < m \le 3\).
Vậy \(m \in \left( { - 1;3} \right]\).
Hướng dẫn giải:
Bước 1: Tính \(\left[ {f\left( {\sqrt {4 - {x^2}} } \right)} \right]'\) và tìm nghiệm của \(\left[ {f\left( {\sqrt {4 - {x^2}} } \right)} \right]' = 0\).
Bước 2: Lập bảng biến thiên của hàm số \(y = f\left( {\sqrt {4 - {x^2}} } \right)\) trên nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) rồi suy ra tập giá trị của \(m\).

