Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ dưới đây.

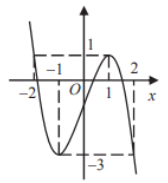
Hỏi phương trình \(f\left( {2 - f\left( x \right)} \right) = 1\) có tất cả bao nhiêu nghiệm thực phân biệt?

Đáp án:

Tọa độ giao điểm của đường thẳng $d:y = 3x$ và parabol $\left( P \right):y = 2{x^2} + 1$ là:

Số giao điểm của đồ thị hàm số $y = {x^3} - 2{x^2} + x - 1$ và đường thẳng $y = 1 - 2x$ là:

Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?

Các đồ thị hàm số $y = {x^4} - 2{x^2} + 2$ và $y =  - {x^2} + 4$ có tất cả bao nhiêu điểm chung?

Số giao điểm của hai đồ thị hàm số $y = 3{x^2}$ và $y = {x^3} + {x^2} + x + 1$ là:

Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x}  + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.

Cho hàm số $y = {x^3} + 3{x^2} + m$ có đồ thị $\left( C \right)$.Để đồ thị $\left( C \right)$ cắt trục hoành tại ba điểm $A,B,C$ sao cho $C$ là trung điểm của $AB$ thì  giá trị của tham số $m$ là: