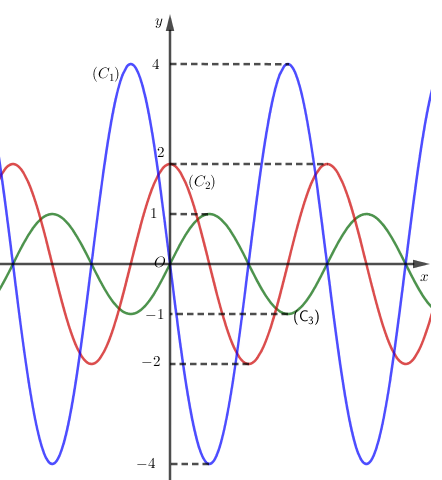
Cho hàm số $y = f(x)$ có đạo hàm cấp một $f'(x)$ và đạo hàm cấp hai $f''(x)$ trên $\mathbb{R}$. Biết đồ thị hàm số $y = f(x),{\mkern 1mu} {\mkern 1mu} y = f'(x),{\mkern 1mu} y = f''(x)$ là một trong các đường cong $({C_1}),({C_2}),({C_3})$ ở hình vẽ bên. Hỏi đồ thị hàm số $y = f(x),{\mkern 1mu} {\mkern 1mu} y = f'(x),{\mkern 1mu} y = f''(x)$ lần lượt theo thứ tự nào dưới đây?

Quan sát dáng đồ thị các hàm số ta thấy đều có dạng đường hình \(\sin \) nên ta dự đoán các hàm số ở đây có thể là dạng \(y = \sin ax\) hoặc \(y = \cos ax\)

Thấy rằng hai đồ thị \(\left( {{C_1}} \right),\left( {{C_3}} \right)\) đi qua điểm \(O\left( {0;0} \right)\) nên một trong hai đồ thị hàm số \(\left( {{C_1}} \right),\left( {{C_3}} \right)\) sẽ là của hàm \(y = f\left( x \right) = \sin ax\), đồ thị \(\left( {{C_2}} \right)\) là của \(y = f'\left( x \right)\) nên loại A và C.

Ta xét hàm số \(y = f\left( x \right) = \sin ax\) có \(f'\left( x \right) = a.\cos ax,f''\left( x \right) =  - {a^2}\sin ax\)

Dễ thấy \(f'\left( 0 \right) = a > 0\).

Quan sát các giá trị trên đồ thị ta dễ dàng nhận ra \(a = 2\).

Vậy ta có các hàm số \(y = \sin 2x,y = 2\cos 2x,y =  - 4\sin 2x\)  lần lượt có đồ thị là \(\left( {{C_3}} \right),\left( {{C_2}} \right),\left( {{C_1}} \right)\)

Vậy \(\left( {{C_3}} \right),\left( {{C_2}} \right),\left( {{C_1}} \right)\) là đồ thị hàm số \(y = f\left( x \right),y = f'\left( x \right),y = f''\left( x \right)\)