Cho hàm số $y = a{x^4} + b{x^2} + c$ có $a > 0,b < 0$. Đồ thị hàm số có $4$ điểm chung với trục hoành nếu:

Hàm số $y = a{x^4} + b{x^2} + c$ có $a > 0,b < 0$ nên có $3$ cực trị và đồ thị của nó có dạng:

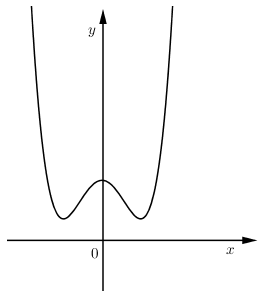
Quan sát đồ thị ta thấy:

- Nếu ${y_{CD}} > 0,{y_{CT}} > 0$ thì đồ thị hàm số không cắt $Ox$ nên điều kiện ${y_{CD}} > 0$ là chưa đủ. 

Do đó A sai.

- Nếu ${y_{CT}} < 0,{y_{CD}} < 0$ thì đồ thị hàm số cắt $Ox$ tại 2 điểm phân biệt nên điều kiện ${y_{CT}} < 0$ là chưa đủ.

Do đó B sai.

- Nếu ${y_{CD}}.{y_{CT}} < 0$ thì ${y_{CT}} < 0 < {y_{CD}}$ nên đường thẳng $y = 0$ cắt đồ thị hàm số tại $4$ điểm phân biệt.

Do đó C đúng.

- Nếu ${y_{CD}}.{y_{CT}} > 0$ thì ${y_{CD}} > {y_{CT}} > 0$ hoặc ${y_{CT}} < {y_{CD}} < 0$ nên đồ thị hàm số không thể cắt $Ox$ tại $4$ điểm phân biệt.

Do đó D sai.