Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới.
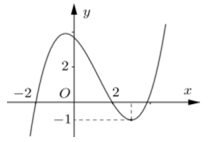
Số nghiệm thực của phương trình \(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{2}{3}\) là
Đáp án
Trả lời bởi giáo viên
Đáp án
Bước 1: Đặt \(t = {x^3} - 3x\), quan sát đồ thị tìm nghiệm của phương trình \(\left| {f\left( t \right)} \right| = \dfrac{2}{3}\) tìm các nghiệm \({t_i}\).
Ta có :\(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{2}{3}\)\( \Leftrightarrow \left[ \begin{array}{l}f\left( {{x^3} - 3x} \right) = \dfrac{2}{3}\\f\left( {{x^3} - 3x} \right) = - \dfrac{2}{3}\end{array} \right.\)
Đặt \(t = {x^3} - 3x\) ta được \(\left[ \begin{array}{l}f\left( t \right) = \dfrac{2}{3}\\f\left( t \right) = - \dfrac{2}{3}\end{array} \right.\)
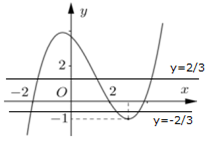
+) Phương trình \(f\left( t \right) = \dfrac{2}{3}\) có ba nghiệm phân biệt \({t_1},\,\,{t_2},\,\,{t_3}\), trong đó \( - 2 < {t_1} < 0 < {t_2} < 2 < {t_3}\).
+) Phương trình \(f\left( t \right) = - \dfrac{2}{3}\) có ba nghiệm phân biệt \({t_4},\,\,{t_5},\,\,{t_6}\), trong đó \({t_4} < - 2 < 2 < {t_5} < {t_6}\) .
Các nghiệm \({t_1},\,\,{t_2},\,\,{t_3},\,\,{t_4},\,\,{t_5},\,\,{t_6}\) phân biệt.
Bước 2: Khảo sát hàm số \(g\left( x \right) = {x^3} - 3x\) suy ra số nghiệm của phương trình \({x^3} - 3x = {t_i}\).
Xét hàm \(g\left( x \right) = {x^3} - 3x\) có \(g'\left( x \right) = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1\)
BBT :
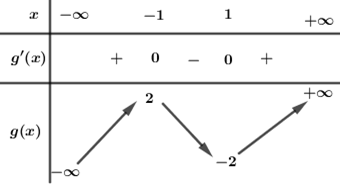
Từ BBT ta thấy :
+) Phương trình \({x^3} - 3x = {t_1} \in \left( { - 2;0} \right)\) có \(3\) nghiệm phân biệt.
+) Phương trình \({x^3} - 3x = {t_2} \in \left( {0;2} \right)\) có \(3\) nghiệm phân biệt.
+) Phương trình \({x^3} - 3x = {t_3} > 2\) có đúng \(1\) nghiệm.
+) Phương trình \({x^3} - 3x = {t_4} < - 2\) có đúng \(1\) nghiệm.
+) Phương trình \({x^3} - 3x = {t_5} > 2\) có đúng \(1\) nghiệm.
+) Phương trình \({x^3} - 3x = {t_6} > 2\) có đúng \(1\) nghiệm.
Vậy phương trình đã cho có tất cả \(3 + 3 + 1 + 1 + 1 + 1 = 10\) nghiệm.
Hướng dẫn giải:
Bước 1: Đặt \(t = {x^3} - 3x\), quan sát đồ thị tìm nghiệm của phương trình \(\left| {f\left( t \right)} \right| = \dfrac{2}{3}\) tìm các nghiệm \({t_i}\).
Bước 2: Khảo sát hàm số \(g\left( x \right) = {x^3} - 3x\) suy ra số nghiệm của phương trình \({x^3} - 3x = {t_i}\).

