Cho hai số phức \(z\) và \(w\) thay đổi thỏa mãn các điều kiện \(\left| {z + 1 + i} \right| = \left| z \right|\) và \(\left| {w - 3 - 4i} \right| = 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = \left| {z - w - 1 - i} \right|\).

+) Giả sử \(z = x + yi\,\,\left( {x,y \in \mathbb{R}} \right),\,\,M\left( {x,y} \right)\) là điểm biểu diễn của số phức \(z\). Ta có:

\(\begin{array}{l}\left| {z + 1 + i} \right| = \left| z \right| \Leftrightarrow \left| {x + yi + 1 + i} \right| = \left| {x + yi} \right|\\ \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = {x^2} + {y^2} \Leftrightarrow x + y + 1 = 0\end{array}\).

\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường thẳng \(d:\,x + y + 1 = 0\).

+) Giả sử \(w + 1 + i = a + bi\,\,\left( {a,b \in \mathbb{R}} \right),\,\,N\left( {a;b} \right)\) là điểm biểu diễn của số phức \(w + 1 + i\). Ta có:

\(\left| {w - 3 - 4i} \right| = 1 \Leftrightarrow \left| {\left( {w + 1 + i} \right) - 4 - 5i} \right| = 1 \Leftrightarrow \left| {a + bi - 4 - 5i} \right| = 1 \Leftrightarrow {\left( {a - 4} \right)^2} + {\left( {b - 5} \right)^2} = 1\).

\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(w + 1 + i\) là đường tròn \(\left( C \right):{\left( {x - 4} \right)^2} + {\left( {y - 5} \right)^2} = 1\) có tâm \(I\left( {4;5} \right)\), bán kính \(R = 1\).

Khi đó ta có:  \(P = \left| {z - w - 1 - i} \right| = \left| {z - \left( {w + 1 + i} \right)} \right| = MN\).

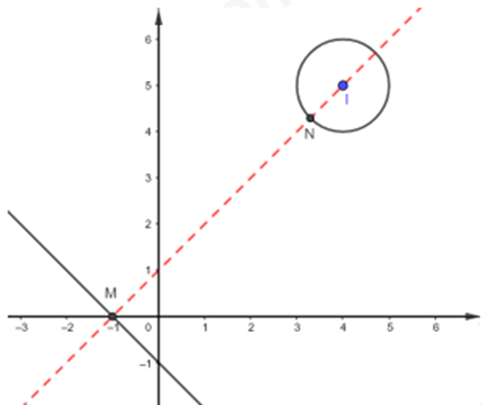
Do đó \({P_{\min }} \Leftrightarrow M{N_{\min }}\).

Khi đó, \(N\) nằm giữa \(I\) và \(M\), đồng thời \(M{N_{\min }} = d\left( {I;d} \right) - R = \dfrac{{\left| {4 + 5 + 1} \right|}}{{\sqrt {{1^2} + {1^2}} }} - 1 = 5\sqrt 2  - 1\).