Câu hỏi:
2 năm trước
Cho đường tròn \(\left( O \right)\) và một dây \(AB\) . Vẽ đường kính \(CD \bot AB\) (\(D\) thuộc cung nhỏ \(AB\) ). Trên cung nhỏ \(BC\) lấy điểm \(M\) . Các đường thẳng \(CM,DM\) cắt đường thẳng \(AB\) lần lượt tại \(E\) và \(F\) . Tiếp tuyến của đường tròn tại \(M\) cắt đường thẳng \(AB\) tại \(N\). Hai đoạn thẳng nào dưới đây không bằng nhau?
Trả lời bởi giáo viên
Đáp án đúng: d
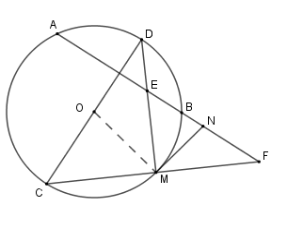
Xét \(\left( O \right)\) có $D$ là điểm chính giữa cung \(AB\) (Vì đường kính \(CD \bot AB\) nên đi qua điểm chính giữa cung \(AB\) )
\(\widehat {NMD} = \dfrac{1}{2}\) sđ \(\overparen{DM}\) (góc tạo bởi tiếp tuyến và dây cung)
\(\widehat {MEN} = \dfrac{1}{2}\) (sđ \(\overparen{MB} + \) sđ \(\overparen{AD}\) )
\( = \dfrac{1}{2}\) (sđ \(\overparen{MB} + \) sđ \(\overparen{BD}\) )
\( = \widehat {NMD}\)
Suy ra \(\Delta MNE\) cân tại \(N \Rightarrow NE = NM\) (*).
Lại có
\(\widehat {NFM} = \widehat {NMF}\)
(vì \(\widehat {NFM} + \widehat {FEM} = 90^\circ \)
\(= \widehat {NMF} + \widehat {NME}\) và \(\widehat {NME} = \widehat {NEM}\) )
Nên \(\Delta NMF\) cân tại \(N \Rightarrow NF = NM\) (**)
Từ (*) và (**) suy ra \(NE = NF = NM\) .
Hướng dẫn giải:
Sử dụng góc có đỉnh bên ngoài đường tròn, góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau
