Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;r} \right)\) nội tiếp tam giác \(ABC\) tiếp xúc với \(BC\) tại \(D\). Vẽ đường kính $DE;$ kéo dài \(AE\) cắt \(BC\) tại \(M\). Chọn câu đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: c
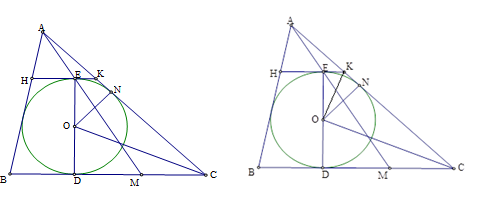
Vẽ tiếp tuyến tại \(E\) của đường tròn \(\left( O \right)\) cắt \(AB,AC\) lần lượt tại \(H,K\).Ta có
\(ED \bot HK,ED \bot BC \Rightarrow HK//BC\).
Gọi \(N\) là tiếp điểm của đường tròn \(\left( O \right)\) tiếp xúc với \(AC\).
\(OK,OC\) là hai tia phân giác của hai góc kề bù \(EON\) và \(NOD\) (tính chất trung tuyến)\( \Rightarrow \widehat {KOC} = {90^0}\).
+ Xét \(\Delta OEK\) và \(\Delta CDO\) có \(\widehat {OEC} = \widehat {CDO}\left( { = {{90}^0}} \right),\widehat {OKE} = \widehat {COD}\) (cùng phụ với \(\widehat {EOK}\)).Do đó \(\Delta OEK \backsim \Delta CDO \Rightarrow \dfrac{{EK}}{{OD}} = \dfrac{{OE}}{{CD}}\) hay \(\dfrac{{EK}}{r} = \dfrac{r}{{CD}}\). Tương tự cũng có \(\dfrac{{HE}}{r} = \dfrac{r}{{BD}}\). Do vậy \(\dfrac{{EK}}{{HE}} = \dfrac{{BD}}{{CD}} \Rightarrow \dfrac{{EK}}{{EK + HE}} = \dfrac{{BD}}{{BD + CD}}\) hay \(\dfrac{{EK}}{{HK}} = \dfrac{{BD}}{{BC}}\) (1)
+ Trong \(\Delta ABM\) có \(HE//BM\), áp dụng hệ quả của định lý Thales trong tam giác ta có \(\dfrac{{HE}}{{BM}} = \dfrac{{AE}}{{AM}}\). Tương tự có \(\dfrac{{EK}}{{CM}} = \dfrac{{AE}}{{AM}}\). Do đó \(\dfrac{{HE}}{{BM}} = \dfrac{{EK}}{{CM}} \Rightarrow \dfrac{{EK}}{{CM}} = \dfrac{{EK + HE}}{{CM + BM}}\) hay \(\dfrac{{EK}}{{CM}} = \dfrac{{HK}}{{BC}} \Rightarrow \dfrac{{EK}}{{HK}} = \dfrac{{CM}}{{BC}}\)
Từ (1) và (2) cho ta \(BD = CM\).
Hướng dẫn giải:
Vẽ tiếp tuyến tại \(E\) của đường tròn \(\left( O \right)\) cắt \(AB,AC\) lần lượt tại \(H,K\).
Sử dụng tam giác đồng dạng và tính chất dãy tỉ số bằng nhau để so sánh.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
