Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB,CD\) là dây cung của \(\left( O \right)\), \(\widehat {COD} = {90^0}\), \(CD\) cắt \(AB\) tại \(M\) (\(D\) nằm giữa \(C\) và \(M\)) và \(OM = 2R\). Tính độ dài các đoạn thẳng \(MD,MC\) theo \(R\).
Trả lời bởi giáo viên
Đáp án đúng: d
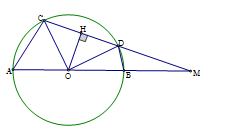
Vì \(\widehat {COD} = {90^0}\) suy ra tam giác
\(COD\) vuông cân tại \(O\) nên \(CD = R\sqrt 2 \).
Gọi \(H\) là trung điểm của \(CD\) suy ra \(OH \bot CD\) (định lý)
Vì \(\Delta HOM\) vuông tại \(H\), \(OH = \dfrac{1}{2}CD = \dfrac{{\sqrt 2 }}{2}R,OM = 2R\).
Trong tam giác vuông \(OMH\) ta có: \(M{H^2} = O{M^2} - O{H^2} = 4{R^2} - \dfrac{{{R^2}}}{2} = \dfrac{{7{R^2}}}{2} \Rightarrow MH = \dfrac{{\sqrt {14} }}{2}R\) suy ra \(MD = MH - AH = \dfrac{{R\sqrt 2 }}{2}\left( {\sqrt 7 - 1} \right)\), \(MC = \dfrac{{R\sqrt 2 }}{2}\left( {\sqrt 7 + 1} \right)\)
Hướng dẫn giải:
Gọi \(H\) là trung điểm của \(CD\)
Dựa vào định lý Pytago để tính toán
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
