Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;R} \right)\), \(AC\) và \(BD\) là hai đường kính . Xác định vị trí của hai đường kính \(AC\) và \(BD\) để diện tích tứ giác \(ABCD\) lớn nhất.
Trả lời bởi giáo viên
Đáp án đúng: a
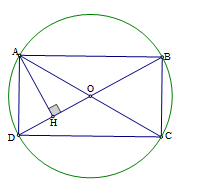
Vẽ \(AH \bot BD\left( {H \in BD} \right)\).
Tứ giác \(ABCD\) có \(OA = OA = R,OB = OD = R\) nên là hình bình hành.
Mà \(AC = BD = 2R\) do đó tứ giác \(ABCD\) là hình chữ nhật, suy ra \({S_{ABCD}} = AB.AD\)
\(\Delta ABD\) có \(\widehat A = {90^0}\), \(AH \bot DB\) nên \(AB.AD = AH.DB\).
Vì \(AH \le AO,DB = 2R\) nên \({S_{ABCD}} \le 2{R^2}\) (không đổi). Dấu “=” xảy ra \( \Leftrightarrow H \equiv O \Leftrightarrow AC \bot BD\).
Vậy khi hai đường kính \(AC\) và \(BD\) vuông góc với nhau thì diện tích tứ giác \(ABCD\) lớn nhất.
Hướng dẫn giải:
+ Vẽ \(AH \bot BD\left( {H \in BD} \right)\)
+ Chứng minh \(ABCD\) là hình chữ nhật
+ Đánh giá \({S_{ABCD}}\) thông qua \({S_{ABD}} = \dfrac{1}{2}AB.AD = \dfrac{1}{2}AH.BD\)
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
