Cho đường tròn có bán kính bằng \(4{\rm{dm}}\) và hai Elip lần lượt nhận đường kính vuông góc nhau của đường tròn làm trục lớn, còn trục bé của mỗi Elip đều bằng \(1{\rm{dm}}\). Tính diện tích của phần hình phẳng tô màu như hình vẽ.

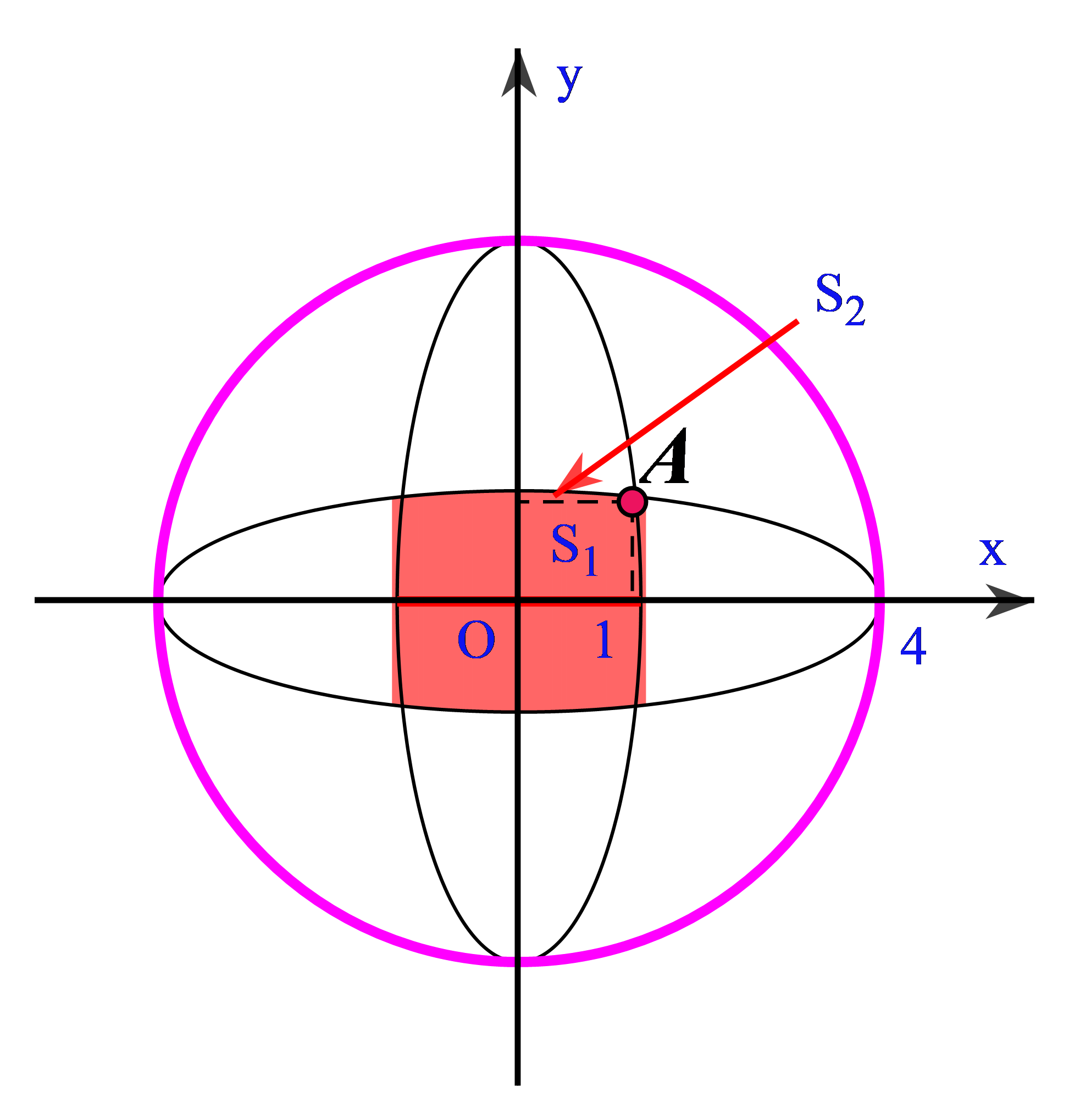
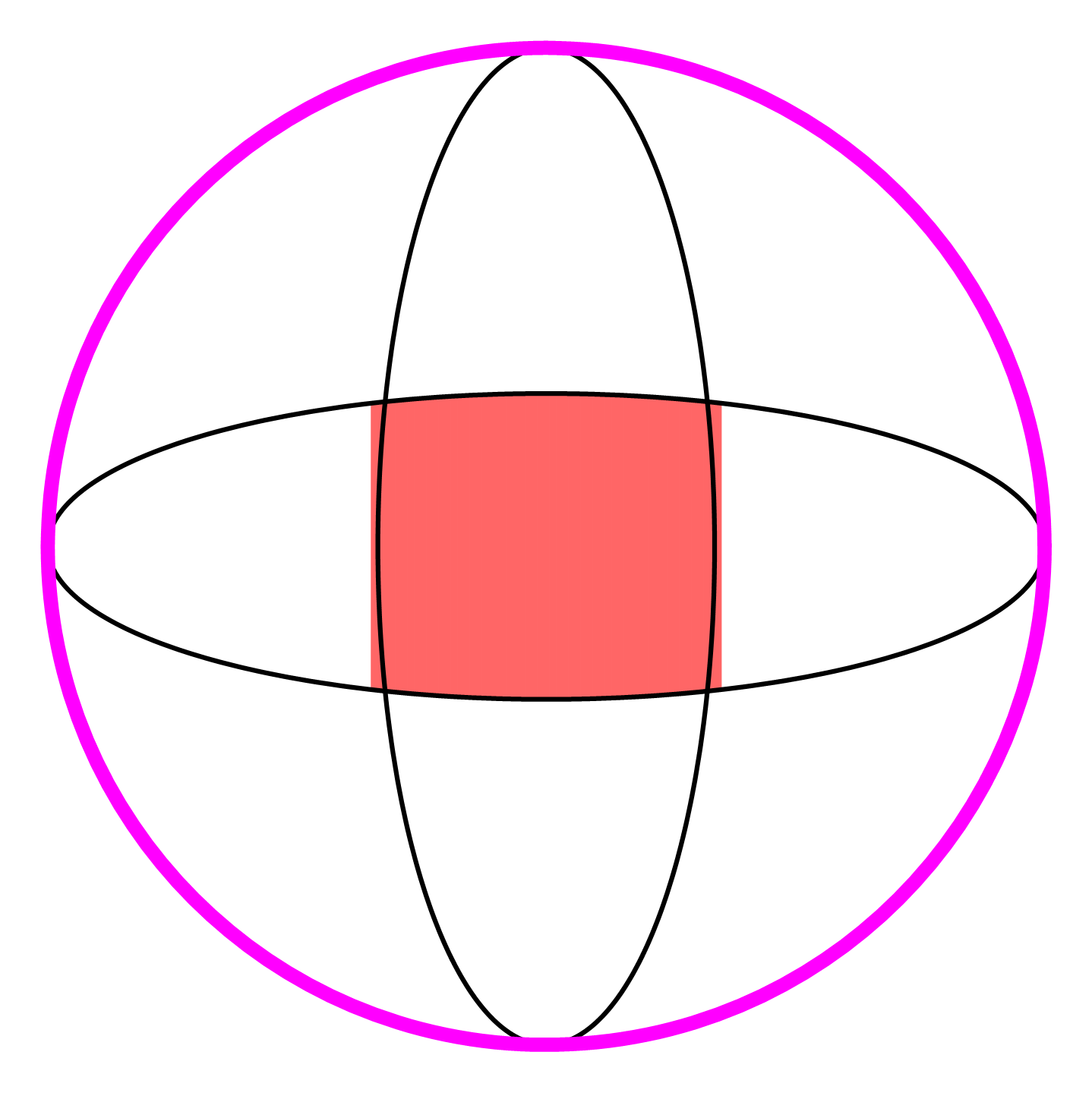
Bước 1: Gắn hệ trục tọa độ. Gọi \(A\left( {{x_A};{y_A}} \right)\) là giao điểm của hai elip trong góc phần tư thứ nhất. Tách diện tích \(\dfrac{1}{4}S = {S_1} + 2{S_2}\).

Gắn hệ trục tọa độ như hình vẽ. Gọi \(A\left( {{x_A};{y_A}} \right)\) là giao điểm của hai elip trong góc phần tư thứ nhất.

Vì tính đối xứng của hình nên $\dfrac{1}{4}$ diện tích cần tính bằng tổng diện tích của \({S_1}\) với hai lần diện tích của \({S_2}\), trong đó \({S_1}\) là hình vuông cạnh \({x_A}\) và \({S_2}\) là diện tích phẳng giới hạn bởi các đường elip (có trục lớn nằm trên trục \(Ox),y = {y_A},x = 0,x = {x_A}\).

Bước 2: Tìm phương trình elip có trục lớn thuộc trục Ox và tính \({S_2}\)

Do tính đối xứng nên \({x_A} = {y_A}\)

Ngoài ra, ta thấy phương trình elip có trục lớn thuộc trục Ox và có $a=4$ và $b=1$

Ta có phương trình \((E):\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{1} = 1.\)

Điểm $A(x_A;y_A)$ thuộc Elip nên ta có: \(\dfrac{{{x_A^2}}}{{16}} + \dfrac{{{x_A^2}}}{1} = 1.\)

\(\Rightarrow {x_A} = \dfrac{4}{{\sqrt {17} }}\).

Khi đó \({S_1} = {\left( {{x_A}} \right)^2} = \dfrac{{16}}{{17}};\) và

\({S_2} = \int_0^{\frac{4}{{\sqrt {17} }}} {\left( {\sqrt {1 - \dfrac{{{x^2}}}{{16}}}  - \dfrac{4}{{\sqrt {17} }}} \right)} dx\)\( = {I_1} - \int_0^{\frac{4}{{17}}} {\dfrac{4}{{\sqrt {17} }}dx}  = {I_1} - \dfrac{{16}}{{17}}\)

Bước 3: Tính \({I_1} = \int_0^{\frac{4}{{\sqrt {17} }}} {\sqrt {1 - \dfrac{{{x^2}}}{{16}}} } dx = \dfrac{1}{4}\int_0^{\frac{4}{{\sqrt {17} }}} {\sqrt {16 - {x^2}} } dx.\) Từ đó tính S.

Xét \({I_1} = \int_0^{\frac{4}{{\sqrt {17} }}} {\sqrt {1 - \dfrac{{{x^2}}}{{16}}} } dx = \dfrac{1}{4}\int_0^{\frac{4}{{\sqrt {17} }}} {\sqrt {16 - {x^2}} } dx.\) Đặt \(x = 4\sin t(0 \le t \le \dfrac{\pi }{2})\)

\( \Rightarrow dx = 4\cos tdt.\)

Đổi cận: \(x = 0 \Rightarrow t = 0;x = \dfrac{4}{{\sqrt {17} }} \Rightarrow t = \arcsin \dfrac{1}{{\sqrt {17} }}.\)

Khi đó, \({I_1} = \dfrac{1}{4}\int_0^{\arcsin \dfrac{1}{{\sqrt {17} }}} {\sqrt {16 - 16{{\sin }^2}t} }  \cdot 4\cos tdt\)\( = 4\int_0^{\sqrt {17} } {{{\cos }^2}} tdt\)\( = 2\int_0^{\arcsin \dfrac{1}{{\sqrt {17} }}} {(1 + \cos 2t)} dt\)\( = \left. {2\left( {t + \dfrac{1}{2}\sin 2t} \right)} \right|_0^{\arcsin }\dfrac{1}{{\sqrt {17} }}\)\( = 2\left( {\arcsin \dfrac{1}{{\sqrt {17} }} + \dfrac{1}{2} \cdot \dfrac{8}{{17}}} \right)\)\( = 2\arcsin \dfrac{1}{{\sqrt {17} }} + \dfrac{8}{{17}}\)

Vậy diện tích cần tìm là

\(S \)\(= 4\left( {\dfrac{{16}}{{17}} + 2\left( {2\arcsin \dfrac{1}{{\sqrt {17} }} + \dfrac{8}{{17}} - \dfrac{{16}}{{17}}} \right)} \right)\)\( = 16\arcsin \dfrac{1}{{\sqrt {17} }}\)