Câu hỏi:
2 năm trước
Cho đoạn mạch xoay chiều như hình vẽ:
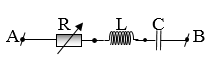
Biết \(L =\dfrac{1}{\pi }H\) ;\(C = \dfrac{{{{10}^{ - 3}}}}{{4\pi }}F\). Đặt vào hai đầu đoạn mạch một hiệu điện thế : \({U_{AB}} = 75\sqrt 2 \cos (100\pi t)(V)\). Công suất trên toàn mạch là \(P=45(W)\). Tính giá trị R?
Trả lời bởi giáo viên
Đáp án đúng: d
\(\begin{gathered}{Z_L} = \omega L = 100\Omega {\text{ }} \hfill \\{Z_{C}} = \dfrac{1}{{\omega C}} = 40\Omega \hfill \\U{\text{ }} = {\text{ }}75{\text{ }}V \hfill \\\end{gathered} \)
Công suất tiêu thụ toàn mạch là:
\(\begin{array}{l}P = \dfrac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R = \dfrac{{{U^2}}}{{{R^2} + {{60}^2}}}\\ \Leftrightarrow 45 = \dfrac{{{{75}^2}}}{{{R^2} + {{60}^2}}} \Leftrightarrow \left[ \begin{array}{l}R = 45\Omega \\R = 80\Omega \end{array} \right.\end{array}\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính cảm kháng, dung kháng: \({Z_L} = \omega L;{Z_{C}} = \dfrac{1}{{\omega C}}\)
+ Vận dụng biếu thức tính công suất tiêu thụ trên toàn mạch: \(P = {I^2}R\)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
