Cho đoạn $AC$ vuông góc với $CE.$ Nối $A$ với trung điểm $D$ của $CE$ và $E$ với trung điểm $B$ của $AC,{\rm{ }}AD$ và $EB$ cắt nhau tại $F.$ Cho $BC = CD = 15{\rm{ }}cm.$ Tính diện tích tam giác $DEF$ theo đơn vị $c{m^2}$ ?
Trả lời bởi giáo viên
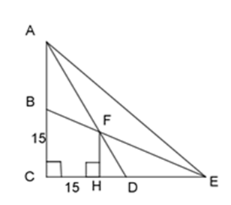
Xét \(\Delta EAC\) có $AD,{\rm{ }}EB$ là 2 đường trung tuyến.
Suy ra $F$ là giao của 2 đường trung tuyến $AD,{\rm{ }}EB$ nên $F$ là trọng tâm của tam giác $ABC.$
\( \Rightarrow \dfrac{{EF}}{{EB}} = \dfrac{{AF}}{{AD}} = \dfrac{2}{3}.\)
Kẻ $FH$ vuông góc với $CE$ ($H$ thuộc $CE$ ).
Xét 2 tam giác vuông $EFH$ và $EBC$ ta có: \(\widehat {BEC}\) chung
\( \Rightarrow \Delta EFH \backsim \Delta EBC\) (g-g)
\( \Rightarrow \dfrac{{EF}}{{EB}} = \dfrac{{FH}}{{BC}} = \dfrac{2}{3} \Rightarrow \dfrac{{FH}}{{15}} = \dfrac{2}{3} \Rightarrow FH = \dfrac{{2.15}}{3} = 10\;cm\)
Vì D là trung điểm của CE nên CD = DE = 15 cm.
Vậy diện tích của tam giác DEF là:
\({S_{\Delta DEF}} = \dfrac{1}{2}.FH.DE = \dfrac{1}{2}.10.15 = 75\;c{m^2}\)
Hướng dẫn giải:
- Kẻ $FH$ vuông góc với $CE$ ($H$ thuộc $CE$ ).
- Chỉ ra hai tam giác đồng dạng
- Áp dụng tính chất đường trung tuyến của tam giác để tìm ra tỉ số của cặp cạnh, suy ra độ dài cạnh FH cần tìm.
- Tính diện tích tam giác $DEF.$