Câu hỏi:
2 năm trước
Cho điểm $M$ và hai phép đối xứng tâm \({O_1}\) và \({O_2}\). Gọi \({D_{{O_1}}}\left( M \right) = {M_1},{D_{{O_2}}}\left( {{M_1}} \right) = {M_2}\), trong các đẳng thức vec tơ sau, đẳng thức nào đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
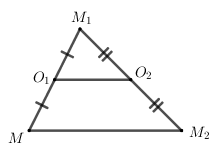
\({D_{{O_1}}}\left( M \right) = {M_1} \Rightarrow {O_1}\) là trung điểm của \(M{M_1}\)
\({D_{{O_2}}}\left( {{M_1}} \right) = {M_2} \Rightarrow {O_2}\) là trung điểm của \({M_1}{M_2}\)
\( \Rightarrow {O_1}{O_2}\) là đường trung bình của tam giác \(M{M_1}{M_2}\)
\( \Rightarrow {O_1}{O_2}//M{M_2}\) và \(2{O_1}{O_2} = M{M_2}\)
\( \Rightarrow \overrightarrow {M{M_2}} = 2\overrightarrow {{O_1}{O_2}} \)
Hướng dẫn giải:
\({D_{{O_1}}}\left( M \right) = {M_1} \Rightarrow {O_1}\) là trung điểm của \(M{M_1}\)
\({D_{{O_2}}}\left( {{M_1}} \right) = {M_2} \Rightarrow {O_2}\) là trung điểm của \({M_1}{M_2}\)
