Câu hỏi:
2 năm trước
Cho điểm \(A\) ở ngoài đường tròn \(\left( {O;R} \right)\). Vẽ cát tuyến \(ABC\) và tiếp tuyến \(AM\) với đường tròn \(\left( O \right)\). \(M\) là tiếp điểm. Chọn câu đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: b
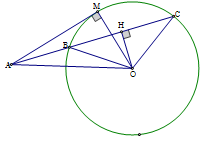
Vẽ \(OH \bot BC,H \in BC\), suy ra \(BH = HC\) (định lý đường kính vuông góc dây cung).
Ta có \(AB + AC = \)\(\left( {AH - BH} \right) + \left( {AH + HC} \right) = 2AH\).
\(\Delta MAO\) có \(\widehat {AMO} = {90^0}\)
Theo định lý Pitago có \(A{M^2} + O{M^2} = O{A^2}\); \(\Delta HAO\) có \(\widehat {AHO} = {90^0}\) nên \(A{H^2} + O{H^2} = O{A^2}\)
Mà \(OB = OM = R\), \(OH \le OB\) nên \(OH \le OM\).
Do đó $O{H^2} \le O{M^2}$, suy ra \(AH \ge AM\). Từ đó ta có: $AB + AC \ge 2AM$.
Hướng dẫn giải:
+ Sử dụng định lý đường kính vuông góc dây cung
+ Sử dụng định lý Pytago và mối quan hệ giữa đường cao và đường xiên để đánh giá.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
