Câu hỏi:
2 năm trước
Cho điểm $A$ không nằm trên mặt phẳng $\left( \alpha \right)$ chứa tam giác $BCD.$ Lấy $E,\,\,F$ là các điểm lần lượt nằm trên các cạnh $AB,\,\,AC.$ Khi $EF$ và $BC$ cắt nhau tại $I,$ chọn kết luận không đúng:
Trả lời bởi giáo viên
Đáp án đúng: d
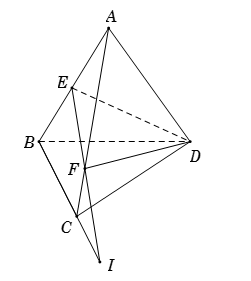
+) Ta có: \(\left( {ABC} \right) \cap \left( {DBC} \right) = BC\), mà \(I \in BC\) nên \(\left( {ABC} \right) \cap \left( {DBC} \right) = BI\) hay A đúng.
+) \(\left( {ABC} \right) \cap \left( {DEF} \right) = EF\) nên B đúng.
+) \(\left( {ABC} \right) \cap \left( {DEF} \right) = EF\), mà \(I \in EF\) nên \(\left( {ABC} \right) \cap \left( {DEF} \right) = EI\) nên C đúng.
+) Dễ thấy \(D\) là điểm chung của \(\left( {DBC} \right)\) và \(\left( {DEF} \right)\), ngoài ra \(I = BC \cap EF\) nên \(\left( {DBC} \right) \cap \left( {DEF} \right) = DI\) nên D sai.
Hướng dẫn giải:
Vẽ hình, tìm giao tuyến của các cặp mặt phẳng ở mỗi đáp án và kết luận.
