Cho \(\Delta ABC.\) Trên tia đối của tia \(BC\) lấy điểm \(E,\) trên tia đối của tia \(CB\) lấy điểm \(F\) sao cho \(BE = CF.\) Gọi \(G\) là trọng tâm tam giác \(ABC.\)\(AG\) cắt \(BC\) tại \(M\). Lấy \(H\) là trung điểm \(AG.\) Nối \(EG\) cắt \(AF\) tại \(N.\) Lấy \(I\) là trung điểm \(EG.\)

Chọn câu đúng.

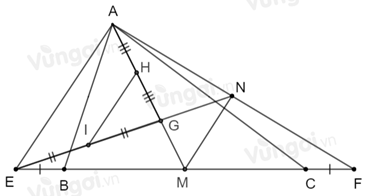
Theo câu trước ta có: \(G\) là trọng tâm \(\Delta AEF\) nên \(EG = \dfrac{2}{3}EN\) (tính chất ba đường trung tuyến của tam giác)

Mà \(GI = \dfrac{1}{2}EG\) (vì \(I\) là trung điểm của \(EG\))

Suy ra \(GI = \dfrac{1}{2}.\dfrac{2}{3}EN = \dfrac{1}{3}EN\)

Mặt khác \(GN = \dfrac{1}{3}EN\) (vì \(G\) là trọng tâm \(\Delta AEF\))

Do đó \(GI = GN\).

Theo câu trước ta có: \(AG = \dfrac{2}{3}AM\) mà \(GH = \dfrac{1}{2}AG\) (vì \(H\) là trung điểm của \(AG\))

Suy ra \(GH = \dfrac{1}{2}.\dfrac{2}{3}AM = \dfrac{1}{3}AM\)

Mặt khác \(GM = \dfrac{1}{3}AM\) (vì \(G\) là trọng tâm \(\Delta AEF\))

Do đó \(GH = GM\).

Xét \(\Delta GHI\) và \(\Delta GMN\) có:

\(GI = GN\) (cmt)

\(\widehat {HGI} = \widehat {NGM}\) (hai góc đối đỉnh)

\(GH = GM\) (cmt)

Vậy \(\Delta GHI = \Delta GMN\,(c.g.c)\) \(\Rightarrow HI = MN\) (hai cạnh tương ứng); \(\widehat {IHG} = \widehat {NMG}\) (hai góc tương ứng)

Mà \(\widehat {IHG};\widehat {NMG}\) ở vị trí so le trong nên \(HI//MN\).