Câu hỏi:
2 năm trước
Cho \(\Delta ABC\), hai đường cao $BD$ và $CE.$ Gọi $M$ là trung điểm của $BC.$ Em hãy chọn câu sai:
Trả lời bởi giáo viên
Đáp án đúng: d
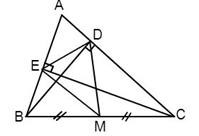
Vì $M$ là trung điểm của $BC$ (gt) suy ra $BM = MC$ (tính chất trung điểm), loại đáp án A.
Xét \({\Delta _v}BCE\)có $M$ là trung điểm của $BC$ (gt) suy ra $EM$ là trung tuyến.
\( \Rightarrow EM = \dfrac{{BC}}{2}\left( 1 \right)\) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Xét \({\Delta _v}BCD\)có $M$ là trung điểm của $BC\left( {gt} \right)$ suy ra $DM$ là trung tuyến.
\( \Rightarrow DM = MB = \dfrac{{BC}}{2}\left( 2 \right)\) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy) nên loại đáp án C.
Từ (1) và (2) \( \Rightarrow EM = DM \Rightarrow \) M thuộc đường trung trực của DE. Loại đáp án B, chọn đáp án D.
Hướng dẫn giải:
Áp dụng tính chất trung điểm của đoạn thẳng, tính chất trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
