Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) có \(AB = AC\). Kẻ \(BN\) là tia phân giác của góc \(B\) \(\left( {N \in AC} \right)\). Kẻ \(CM\) là tia phân giác của góc \(C\) \(\left( {M \in AB} \right)\), \(CM\) và \(BN\) cắt nhau tại \(I.\) So sánh \(IC\) và \(IB?\)
Trả lời bởi giáo viên
Đáp án đúng: c
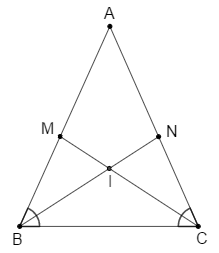
\(\Delta ABC\) có \(AB = AC\) nên \(\Delta ABC\) cân tại \(A\) suy ra \(\widehat B = \widehat C\) (tính chất tam giác cân) (1)
\(BN\) là phân giác của \(\widehat B\) nên \(\widehat {IBC} = \dfrac{{\widehat B}}{2}\) (1)
\(CM\) là phân giác của \(\widehat C\) nên \(\widehat {ICB} = \dfrac{{\widehat C}}{2}\) (2)
Từ (1), (2) và (3) ta có \(\widehat {IBC} = \widehat {ICB}\) do đó \(\Delta IBC\) cân tại \(I\) suy ra \(IB = IC\) (tính chất tam giác cân).
Hướng dẫn giải:
- Sử dụng: Tính chất tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
