Câu hỏi:
2 năm trước
Cho biểu thức $P = \dfrac{{10x}}{{{x^2} + 3x - 4}} - \dfrac{{2x - 3}}{{x + 4}} + \dfrac{{x + 1}}{{1 - x}}$
Tìm $x \in \mathbb{Z}$ để $P + 1 \in \mathbb{Z}$.
Trả lời bởi giáo viên
Đáp án đúng: b
Theo câu trước ta có $P = \dfrac{{ - 3x + 7}}{{x + 4}}$ với \(x \ne 1;x \ne -4\), nên
$P + 1 = \dfrac{{ - 3x + 7}}{{x + 4}} + 1 = \dfrac{{ - 3x + 7 + x + 4}}{{x + 4}} = \dfrac{{ - 2x + 11}}{{x + 4}} = - 2 + \dfrac{{19}}{{x + 4}}$
$x \in Z$ để $P + 1 \in Z \Rightarrow \left( {x + 4} \right) \in U\left( {19} \right) = \left\{ { \pm 1;\, \pm 19} \right\}$
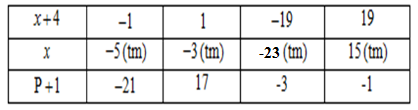
Vậy $x \in \left\{ { - 23; - 5; - 3;15} \right\}$ thì $P + 1 \in Z$.
Hướng dẫn giải:
+) Tìm ĐKXĐ của P.
+) Tách \(P\) về dạng \(P = a + \dfrac{b}{{MS}},\,\,a,\,\,b \in Z.\)
+) Đề \(P \in Z\) thì \(\dfrac{b}{{MS}} \in Z \Leftrightarrow MS \in U\left( b \right).\)
+) Tìm U(b) sau đó lập bảng, giải phương trình tìm x.
+) Xét xem các giá trị của x có thỏa mãn ĐKXĐ của bài toán hay không rồi kết luận x.
Giải thích thêm:
Vì $1 \in Z$ nên để $P+1 \in Z$ thì $ P \in Z$ nên các em có thể tìm $x \in Z$ để $ P \in Z.$
