Cho hình vẽ sau:
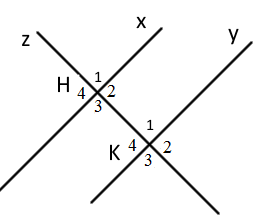
Em hãy chọn phát biểu đúng trong các phát biểu sau:
\(\widehat {{H_1}}\) và \(\widehat {{K_1}}\) là hai góc so le trong (sai, vì đó là 2 góc đồng vị, loại đáp án A)
\(\widehat {{H_4}}\) và \(\widehat {{K_4}}\) là hai góc đồng vị (đúng, chọn B)
\(\widehat {{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài (sai, vì đó là 2 góc trong cùng phía, loại đáp án C)
\(\widehat {{H_4}}\) và \(\widehat {{K_2}}\) là hai góc so le trong (sai, vì đó là 2 góc so le ngoài, loại đáp án D)
Cho hình bình hành ABCD có \(\widehat D = 56^\circ \). Tia Bd là tia phân giác của \(\widehat {ABC}\), cắt AD tại E. Tính số đo góc BED?
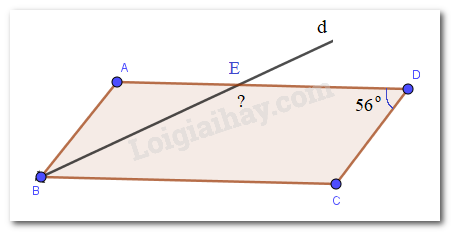
Vì ABCD là hình bình hành nên \(\widehat {ABC} = \widehat {ADC}\)( tính chất hình bình hành), mà \(\widehat {ADC} = 56^\circ \Rightarrow \widehat {ABC} = 56^\circ \)
Vì Bd là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {ABE} = \widehat {CBE} = \frac{1}{2}.\widehat {ABC} = \frac{1}{2}.56^\circ = 28^\circ \)
Vì ABCD là hình bình hành nên AD // BC ( tính chất hình bình hành)
\( \Rightarrow \widehat {AEB} = \widehat {CBE}\) ( 2 góc so le trong)
\( \Rightarrow \widehat {AEB} = 28^\circ \)
Ta có: \(\widehat {AEB} + \widehat {BED} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 28^\circ + \widehat {BED} = 180^\circ \\ \Rightarrow \widehat {BED} = 180^\circ - 28^\circ = 152^\circ \end{array}\)
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.

Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {35^0} = {145^0}\)
Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong
Mặt khác, đường thẳng d cắt 2 đường thẳng x và y tạo thành 1 cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\) nên cặp góc so le trong còn lại cũng bằng nhau
\( \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {145^0}.\)
Cho hình vẽ sau:
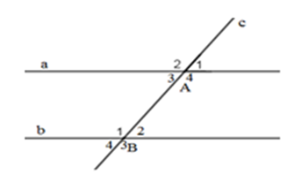
Biết \(\widehat {{A_3}} = \widehat {{B_2}} = {30^0}\). Tính số đo góc \({A_4}\) và góc \({B_1}.\)
Cặp góc so le trong còn lại là: \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\).
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {30^0} = {150^0}\\ \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {150^0}\end{array}\)
Cho hình sau, biết a // b.
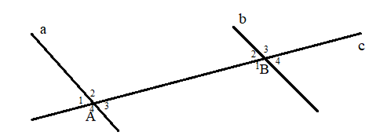
Phát biểu không đúng là:
Vì a // b nên:
\(\widehat {{A_1}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{A_1}} + \widehat {{B_3}} = 180^\circ \) nên khẳng định A đúng
\(\widehat {{A_2}} = \widehat {{B_1}}\) ( 2 góc so le trong) nên khẳng định B đúng
\(\widehat {{A_4}} = \widehat {{B_1}}\) (2 góc đồng vị), mà \(\widehat {{B_1}} + \widehat {{B_4}} = 180^\circ \)( 2 góc kề bù) nên \(\widehat {{A_4}} + \widehat {{B_4}} = 180^\circ \) nên khẳng định C sai
\(\widehat {{A_3}} = \widehat {{B_4}}\)( 2 góc đồng vị) nên khẳng định D đúng

