Xét \({z_1},{z_2}\) là các số phức thay đổi thoả mãn \(\left| {\overline {{z_1}}  - 3 + 2i} \right| = \left| {\overline {{z_2}}  - 3 + 2i} \right| = 2\) và \(\left| {{z_1} - {z_2}} \right| = 2\sqrt 3 \). Gọi $m, n$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(\left| {{z_1} + {z_2} - 3 - 5i} \right|\). Khi đó \(m + 2n\) bằng

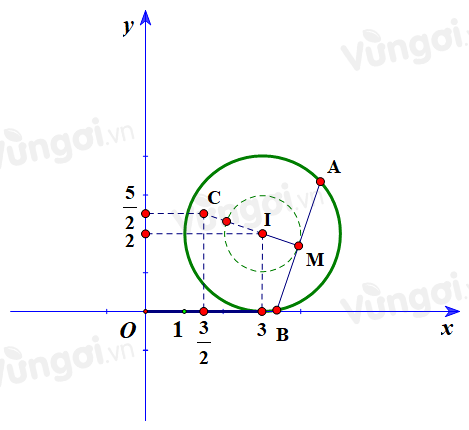
Gọi $A, B$ và \(C\) lần lượt là điểm biểu diễn cho \({z_1},{z_2}\) và \(\dfrac{3}{2} + \dfrac{{5i}}{2}\).

Ta có

\(\begin{array}{l}\left| {\overline {{z_1}}  - 3 + 2i} \right| = \left| {\overline {{z_2}}  - 3 + 2i} \right| = 2\\\Leftrightarrow \left| {\overline {{z_1}}-\overline {  (3 + 2i)} } \right| = \left| {\overline {{z_2}} -\overline {(3 + 2i)} } \right| = 2\\ \Leftrightarrow \left| {\overline {{z_1} - (3 + 2i)} } \right| = \left| {\overline {{z_2} - (3 + 2i)} } \right| = 2\end{array}\)

\( \Leftrightarrow \left| {{z_1} - (3 + 2i)} \right| = \left| {{z_2} - (3 + 2i)} \right| = 2\)

Do đó $A, B$ thuộc đường tròn tâm \(I(3;2)\), bán kính \(R = 2\), và từ \(\left| {{z_1} - {z_2}} \right| = 2\sqrt 3 \) ta được \(AB = 2\sqrt 3 \).

Gọi \(M\) là trung điểm của $A B$ thì \(IM = \sqrt {I{A^2} - M{A^2}}  = \sqrt {{2^2} - 3}  = 1\) nên \(M\) thuộc đường tròn tâm \(I\), bán kính \(r = 1\).

Khi đó \(P = \left| {{z_1} + {z_2} - 3 - 5i} \right|\) \( = 2\left| {\dfrac{{{z_1} + {z_2}}}{2} - \left( {\dfrac{3}{2} + \dfrac{{5i}}{2}} \right)} \right| = 2MC\).

\(P\) đạt giá trị lớn nhất và giá trị nhỏ nhất lần lượt bằng \(m = 2(IC + r) = \sqrt {10}  + 2\) và \(n = \) \(2(IC - r) = \sqrt {10}  - 2\).

Suy ra \(m + 2n = 3\sqrt {10}  - 2.\)