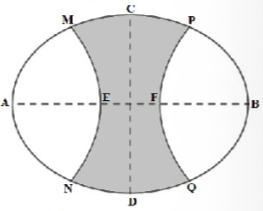
Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh \(A,B,C,D\) và hai đường parabol có các đỉnh lần lượt là \(E,F\) (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng \(AB\), đối xứng với nhau qua trục \(CD\), hai parabol cắt elip tại các điểm \(M,N,P,Q\). Biết \(AB = 8m,CD = 6m,MN = PQ = 3\sqrt 3 m,EF = 2m\). Chi phí để trồng hoa trên vườn là \(300.000\) đ/m2 . Hỏi số tiền trồng hoa cho cả vườn gần nhất với số tiền nào dưới đây?
Trả lời bởi giáo viên
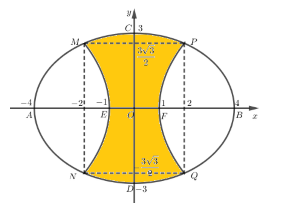
Gắn hệ trục tọa độ như hình vẽ, dễ thấy \(B\left( {4;0} \right),C\left( {0;3} \right),F\left( {1;0} \right)\).
Ta chỉ cần xét phần bên phải trục \(Oy\) vì hình vẽ có tính đối xứng.
Phương trình elip: \(\left( E \right):\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1 \Rightarrow x = 4\sqrt {1 - \dfrac{{{y^2}}}{9}} \).
Dễ thấy \(PQ = 3\sqrt 3 \Rightarrow P\left( {m;\dfrac{{3\sqrt 3 }}{2}} \right)\) với \(m > 0\).
Mà \(P \in \left( E \right) \Rightarrow m = 4\sqrt {1 - \dfrac{{27/4}}{9}} = 2 \Rightarrow P\left( {2;\dfrac{{3\sqrt 3 }}{2}} \right)\).
Gọi phương trình parabol bên phải trục tung là \(\left( P \right):x = a{y^2} + by + c\).
Đỉnh \(F\left( {1;0} \right) \Rightarrow c = 1,b = 0 \Rightarrow x = a{y^2} + 1\)
\(P \in \left( P \right):x = a{y^2} + 1 \Leftrightarrow 2 = a.{\left( {\dfrac{{3\sqrt 3 }}{2}} \right)^2} + 1 \Leftrightarrow \dfrac{{27}}{4}a + 1 = 2 \Leftrightarrow a = \dfrac{4}{{27}}\) \( \Rightarrow \left( P \right):x = \dfrac{4}{{27}}{y^2} + 1\).
Diện tích hình phẳng giới hạn bởi elip \(\left( E \right)\) và parabol \(\left( P \right)\) (phần màu trắng) nên phải trục tung là:
\({S_1} = \int\limits_{ - \dfrac{{3\sqrt 3 }}{2}}^{\dfrac{{3\sqrt 3 }}{2}} {\left[ {4\sqrt {1 - \dfrac{{{y^2}}}{9}} - \dfrac{4}{{27}}{y^2} - 1} \right]dy} \)\( \Rightarrow 2{S_1} \approx 21,6686\)
Diện tích elip: \(S = \pi ab = \pi .4.3 = 12\pi \).
Diện tích phần tô màu đậm là \(S - 2{S_1} \approx 16,03\).
Số tiền trồng hoa là: \(16,03.300.000 = 4.809.000\)
Hướng dẫn giải:
- Viết phương trình elip và parabol.
- Tính diện tích hình phẳng (phần màu trắng) giới hạn bởi nửa elip bên phải trục \(CD\) và parabol bên phải trục \(CD\).


