Câu hỏi:
2 năm trước
Tứ giác \(ABCD\) có \(E,F\) theo thứ tự là trung điểm của \(BD,AC.\) Gọi \(I\) là trung điểm của \(EF.\) Gọi \(M,N,P\) lần lượt là chân đường vuông góc kẻ từ \(A,B,I\) đến \(CD.\) Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: c
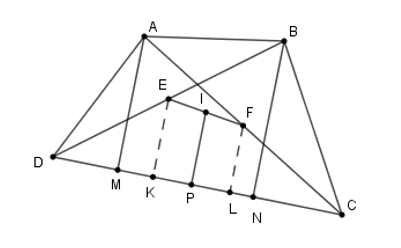
Gọi \(K,L\) lần lượt là chân đường vuông góc kẻ từ \(E,F\) đến \(DC\).
Suy ra \(AM//EK//IP//FL//BN\).
Xét tam giác \(ACM\) có \(F\) là trung điểm \(AC\) và \(FL//AM \Rightarrow L\) là trung điểm \(CM\)
Suy ra \(FL\) là đường trung bình của tam giác \(ACM \Rightarrow AM = 2FL\) (1)
Xét tam giác \(BDN\) có \(E\) là trung điểm \(BD\) và \(EK//NB \Rightarrow K\) là trung điểm \(DN\).
Suy ra \(EK\) là đường trung bình của tam giác \(BDN \Rightarrow BN = 2EK\) (2)
Xét tứ giác \(EKLF\) có \(EK//FL\) nên \(EKLF\) là hình thang.
Lại có: \(EK//IP//FL;\,IE = IF \Rightarrow PL = PK\).
Suy ra \(IP\) là đường trung bình của hình thang \(EFLK \Rightarrow EK + FL = 2IP\).
\( \Rightarrow 2EK + 2FL = 4IP\,\,\,\left( 3 \right)\)
Từ (1), (2), (3) suy ra \(AM + BN = 4IP\).
Hướng dẫn giải:
Gọi \(K,L\) lần lượt là chân đường vuông góc kẻ từ \(E,F\) đến \(DC\).
Sử dụng tính chất đường trung bình của tam giác và đường trung bình của hình thang.
