Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 27\). Gọi \(\left( \alpha  \right)\) là mặt phẳng đi qua hai điểm \(A\left( {0;0; - 4} \right)\), \(B\left( {2;0;0} \right)\) và cắt \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) sao cho khối nón đỉnh là tâm của \(\left( S \right)\) và đáy là đường tròn \(\left( C \right)\) có thể tích lớn nhất. Biết rằng \(\left( \alpha  \right):ax + by - z + c = 0\), khi đó \(a - b + c\) bằng

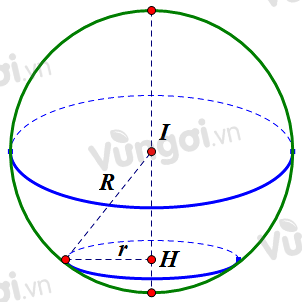
Mặt cầu \(\left( S \right)\) có tâm \(I\left( {1; - 2;3} \right)\) và bán kính \(R = 3\sqrt 3 \).

Vì \(\left( \alpha  \right):ax + by - z + c = 0\) đi qua hai điểm \(A\left( {0;0; - 4} \right)\), \(B\left( {2;0;0} \right)\) nên \(c =  - 4\) và \(a = 2\).

Suy ra \(\left( \alpha  \right):2x + by - z - 4 = 0\).

Đặt \(IH = x\), với \(0 < x < 3\sqrt 3 \) ta có bán kính của \(\left( C \right)\) là \(r = \sqrt {{R^2} - {x^2}}  = \sqrt {27 - {x^2}} \).

Thể tích khối nón là \(V = \dfrac{1}{3}\pi {r^2}.IH = \dfrac{1}{3}\pi \left( {27 - {x^2}} \right).x\) \( = \dfrac{1}{{3\sqrt 2 }}\pi \sqrt {\left( {27 - {x^2}} \right) \cdot \left( {27 - {x^2}} \right) \cdot 2{x^2}} \)\(  \le 18\pi \).

\({V_{\max }} = 18\pi \) khi \(27 - {x^2} = 2{x^2} \Leftrightarrow x = 3\).

Khi đó, \(d\left( {I,\left( \alpha  \right)} \right) = \dfrac{{\left| {2b + 5} \right|}}{{\sqrt {{b^2} + 5} }} = 3 \Leftrightarrow {\left( {2b + 5} \right)^2} \)\(= 9\left( {{b^2} + 5} \right) \Leftrightarrow b = 2\).

Vậy \(a - b + c =  - 4\).