Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình chữ nhật. Biết \(AD = 2a\), \(SA = a\). Khoảng cách từ \(A\) đến \(\left( {SCD} \right)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
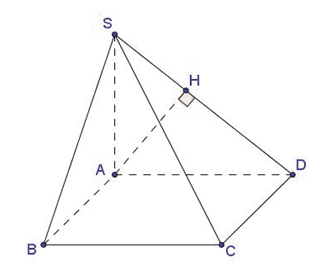
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \)\(\Rightarrow \left( {SCD} \right) \bot \left( {SAD} \right)\).
Kẻ \(AH \bot SD\) suy ra \(AH \bot \left( {SCD} \right)\).
\(d\left( {A,\left( {SCD} \right)} \right) = AH = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} \)\(= \dfrac{{2a}}{{\sqrt 5 }}\).
Hướng dẫn giải:
Bước 1: Kẻ \(AH \bot SD\), chứng minh \(AH \bot \left( {SCD} \right)\).
Bước 2: Sử dụng hệ thức lượng trong tam giác vuông tính AH.