Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), \(SA\) vuông góc với mặt phẳng đáy. Tính cosin góc giữa hai đường thẳng \(SD\) và \(BC\), biết \(AD = DC = a\), \(AB = 2a\), \(SA = \dfrac{{2a\sqrt 3 }}{3}\).

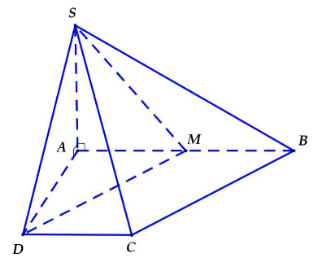
Gọi \(M\) là trung điểm \(AB\). Ta có \(MB = DC = a\). Mà \(MB\,{\rm{//}}\,CD\) nên \(MBCD\) là hình bình hành. Do đó \(DM\,{\rm{//}}\,BC\). Suy ra \(\left( {\widehat {SD,BC}} \right) = \left( {\widehat {SD,DM}} \right)\).

\(SM = \sqrt {S{A^2} + A{M^2}}  = \dfrac{{a\sqrt {21} }}{3}\), \(DM = \sqrt {A{M^2} + A{D^2}}  = a\sqrt 2 \), \(SD = \sqrt {S{A^2} + A{D^2}}  = \dfrac{{a\sqrt {21} }}{3}\).

Áp dụng định lí cosin trong \(\Delta SDM\) ta được \({\rm{cos}}\widehat {SDM} = \dfrac{{S{D^2} + D{M^2} - S{M^2}}}{{2SD.DM}} \)\(= \dfrac{3}{{\sqrt {42} }}\).

Suy ra \(\cos \left( {\widehat {SD,BC}} \right) = \dfrac{3}{{\sqrt {42} }}\).