Câu hỏi:
2 năm trước
Trong chân không, cho hai điện tích \({q_1} = - {q_2} = {10^{ - 7}}C\) đặt tại hai điểm $A$ và $B$ cách nhau $8cm$. Tại điểm $C$ nằm trên đường trung trực của $AB$ và cách $AB$ $3cm$ người ta đặt điện tích \({q_o} = {10^{ - 7}}C\). Lực điện tổng hợp tác dụng lên $q_0$.
Trả lời bởi giáo viên
Đáp án đúng: a
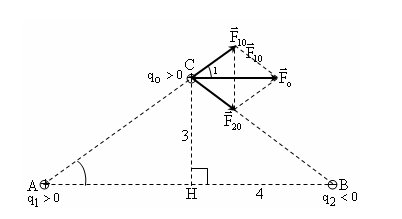
Vị trí các điện tích như hình vẽ.
+ Lực do q1 tác dụng lên qo:
\({F_{10}} = k\dfrac{{\left| {{q_1}{q_0}} \right|}}{{A{C^2}}} = {9.10^9}\dfrac{{\left| {{{10}^{ - 7}}{{.10}^{ - 7}}} \right|}}{{0,{{05}^2}}} = 0,036N\)
+ Lực do q2 tác dụng lên qo:
\({F_{20}} = {F_{10}} = 0,036N\) ( do \(\left| {{q_1}} \right| = \left| {{q_2}} \right|\))
+ Do \({F_{20}} = {F_{10}}\) nên hợp lực Fo tác dụng lên qo:
\({F_o} = 2{F_{10}}.\cos {C_1} = 2.{F_{10}}.\cos A = 2.{F_{10}}.\dfrac{{AH}}{{AC}}\)
\({F_o} = 2.0,036.\dfrac{4}{5} = 57,{6.10^{ - 3}}N\)
+ Vậy có phương // AB, cùng chiều với vectơ \(\overrightarrow {AB} \) (hình vẽ) và có độ lớn:
\({F_o} = 57,{6.10^{ - 3}}N\)
Hướng dẫn giải:
+ Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
+ Phương pháp tổng hợp lực
+ Vận dụng hệ thức lượng trong tam giác
