Trả lời bởi giáo viên
Đáp án đúng: d
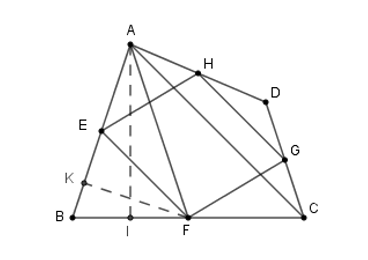
Gọi \(FK \bot AB\) tại \(K,\,AI \bot BC\) tại \(I\).
Ta có: \({S_{BEF}} = \dfrac{1}{2}FK.BE\) và \({S_{FAB}} = \dfrac{1}{2}FK.AB\) mà \(AB = 2EB\) (do \(E\) là trung điểm của \(AB\)) nên \({S_{BEF}} = \dfrac{1}{2}FK.\dfrac{1}{2}AB = \dfrac{1}{2}\left( {\dfrac{1}{2}FK.AB} \right) = \dfrac{1}{2}{S_{ABF}}\) (1)
Lại có: \({S_{ABC}} = \dfrac{1}{2}AI.BC;\,\) \({S_{ABF}} = \dfrac{1}{2}AI.BF = \dfrac{1}{2}AI.\dfrac{1}{2}BC = \dfrac{1}{2}\left( {\dfrac{1}{2}AI.BC} \right) = \dfrac{1}{2}{S_{ABC}}\) (2)
Từ (1) và (2) suy ra: \({S_{BEF}} = \dfrac{1}{2}{S_{ABF}} = \dfrac{1}{2}.\dfrac{1}{2}{S_{ABC}} = \dfrac{1}{4}{S_{ABC}}.\)
Tỉ số cần tìm là \(\dfrac{1}{4}.\)
Hướng dẫn giải:
Sử dụng công thức tính diện tích tam giác \(S = \dfrac{1}{2}ah\).

