Trả lời bởi giáo viên
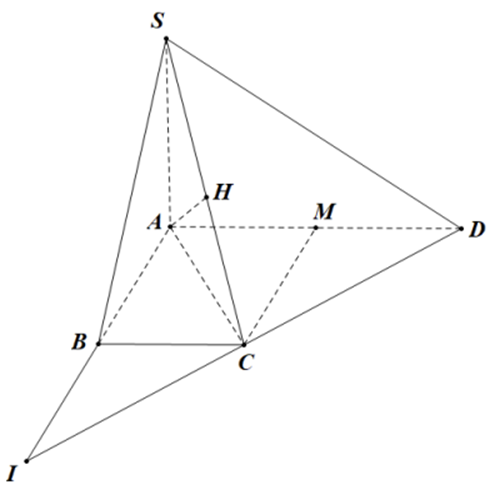
Ta có: \(\left\{ \begin{array}{l}CB \bot SA\\CB \bot AB\end{array} \right. \Rightarrow CB \bot \left( {SAB} \right)\). Góc giữa SC và (SAB) bằng góc \(\widehat {CSB} = {30^o}\)
Lại có tam giác SBC vuông tại B nên ta có: \(SB = \dfrac{{BC}}{{\tan {{30}^o}}} = a\sqrt 3 \) do đó \(SA = a\sqrt 2 \)
\(AB \cap CD = I\)\( \Rightarrow AB \cap \left( {SCD} \right) = I\)
I đối xứng A qua B
\(\dfrac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {A;\left( {SCD} \right)} \right)}} = \dfrac{{BI}}{{AI}} = \dfrac{1}{2}\)\( \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SCD} \right)} \right)\)
\(\Delta SAC\)vuông cân tại A \( \Rightarrow AH = \dfrac{{SA}}{{\sqrt 2 }} = a\)
Gọi H là trung điểm của SC.
\( \Rightarrow \left\{ \begin{array}{l}AH \bot SC\\AH \bot CD\end{array} \right. \Rightarrow AH \bot \left( {SAC} \right)\)\( \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = AH\)
Vậy \(d\left( {B;\left( {SCD} \right)} \right) = \dfrac{1}{2}AH = a\)
Hướng dẫn giải:
- Tính góc \(\widehat {CSB}\)
- Tính SA
- Gọi H là trung điểm của SC.
- Chứng minh \(d\left( {B;\left( {SCD} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SCD} \right)} \right)\)
- Tính AH.
Câu hỏi khác
- Đề thi thử phần Toán ĐGTD Đại học Bách Khoa Hà Nội lần 1, có đáp án và lời giải chi tiết
- Đề thi thử phần Toán ĐGTD Đại học Bách Khoa Hà Nội lần 2, có đáp án và lời giải chi tiết
- Đề thi chính thức ĐGTD Bách khoa 2022 - mã 103 có đáp án và lời giải chi tiết
- Đề thi thử ĐGTD Bách khoa trường Yên Lạc - Lần 2 có đáp án và lời giải chi tiết
