Cho tam giác $A B C$ vuông tại \(A,AB = a,ABC = {60^o}\). Tính thể tích của khối tròn xoay sinh bởi tam giác $ABC$ khi quay quanh đường thẳng $B C$
Trả lời bởi giáo viên
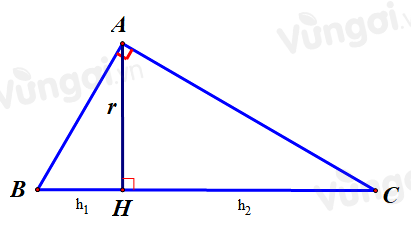
Kẻ $AH$ vuông góc với $AB$
Khi đó quay tam giác \(ABC\) vuông tại \(A\) quanh cạnh \(BC\) thu được 2 khối nón có chiều cao lần lượt là $HB$ và \(HC\) và bán kính là $r=AH$, gọi hai hình nón đó lần lượt là \({V_1};{V_2}\)
Ta có: $AB=a$
\(\begin{array}{l}BC = 2AB = 2a\\AH = \dfrac{{AB\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{2}\end{array}\)
Ta có:
\(\begin{array}{l}{V_1} = \dfrac{1}{3}\pi {r^2}{h_1};{V_2} = \dfrac{1}{3}\pi {r^2}{h_2}\\V = {V_1} + {V_2} = \dfrac{1}{3}\pi {r^2}.\left( {{h_1} + {h_2}} \right)\\ = \dfrac{1}{3}\pi .\dfrac{{3{a^2}}}{4}.2a = \dfrac{{\pi {a^3}}}{2}\end{array}\)
Hướng dẫn giải:
- Quay tam giác \(ABC\) vuông tại \(A\) quanh cạnh \(BC\) thu được 2 khối nón có chiều cao lần lượt là $HB$ và \(HC\)
- Áp dụng công thức tính thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\)là \(V = \dfrac{1}{3}\pi {r^2}h\).

