Trả lời bởi giáo viên
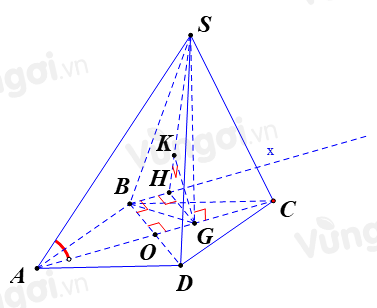
Kẻ Bx song song với AC.
Kẻ GH vuông góc với Bx, GK vuông góc với SH
Bước 1: Chứng minh \(GK \bot \left( {SBH} \right)\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}GH \bot BH\\BH \bot SG\end{array} \right\} \Rightarrow BH \bot \left( {SGH} \right)\\\left. \begin{array}{l} \Rightarrow BH \bot GK\\GK \bot SH\end{array} \right\} \Rightarrow GK \bot \left( {SHB} \right)\end{array}\)
Bước 2: Chứng minh \(d\left( {AC,SB} \right) = GK\)
Ta có BH//AC \( \Rightarrow AC//\left( {SHB} \right)\)
Mà \(SB \subset \left( {SHB} \right)\)
\( = > d\left( {SB,AC} \right)\)\( = d\left( {AC,\left( {SHB} \right)} \right)\)\( = d\left( {G,\left( {SHB} \right)} \right) = GK\)
Bước 3: Tính GK
Dễ thấy tứ giác OBHG là hình chữ nhật
=> \(HG = OB = \dfrac{a}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SGH ta có:
\(\dfrac{1}{{G{K^2}}} = \dfrac{1}{{S{G^2}}} + \dfrac{1}{{G{H^2}}}\)\( = \dfrac{1}{{4{a^2}}} + \dfrac{4}{{{a^2}}} = \dfrac{{17}}{{4{a^2}}}\)
\( \Rightarrow GK = \dfrac{{2\sqrt {17} a}}{{17}}\)
Vậy \(d\left( {SB,AC} \right) = \dfrac{{2a\sqrt {17} }}{{17}}\)
Hướng dẫn giải:
Kẻ Bx song song với AC. Kẻ GH vuông góc với Bx, GK vuông góc với SH
Bước 1: Chứng minh \(GK \bot \left( {SBH} \right)\)
Bước 2: Chứng minh \(d\left( {AC,SB} \right) = GK\)
Bước 3: Tính GK