Xét các số phức z thỏa mãn $\left| {z - i} \right| = \left| {z + 3i} \right|$. Giá trị nhỏ nhất của biểu thức$\left| {z + 2 - i} \right| + \left| {z - 3 - 3i} \right|$ bằng

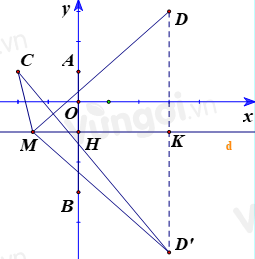
Bước 1: Tìm tập hợp biểu diễn số phức thỏa mãn $\left| {z - i} \right| = \left| {z + 3i} \right|$ và biểu diễn trên mặt phẳng tọa độ.

Gọi $A\left( {0;1} \right)$ là điểm biểu diễn số phức $i$

$B\left( {0; - 3} \right)$ là điểm biểu diễn số phức $- 3i$

$M\left( {a;b} \right)$ là điểm biểu diễn số phức $z = a + bi$

Khi đó $\left| {z - i} \right| = \left| {z + 3i} \right|$ tương đương với điểm M là điểm thỏa mãn: MA=MB

Khi đó tập hợp điểm M là đường trung trực d của đoạn thẳng AB.

Gọi H là trung điểm của AB=>H(0;-1)

Ta có đường thẳng d: y=-1.

Bước 2: Biểu diễn số phức ${z_1} =  - 2 + i;{z_2} = 3 + 3i$ trên mặt phẳng tọa độ và tìm giá trị nhỏ nhất của $\left| {z - {z_1}} \right| + \left| {z - {z_2}} \right|$

Gọi C, D lần lượt là điểm biểu diễn số phức ${z_1} =  - 2 + i;{z_2} = 3 + 3i$

Khi đó bài toán trở thành tìm giá trị nhỏ nhất của MC+MD.

Lấy điểm D’ đối xứng D qua D.

$\Rightarrow MC + MD = MC + MD' \le CD'$

Đường thẳng DD’ qua D và vuông góc với đường thẳng d có phương trình là:x=3

=> Giao điểm của DD’ và d là K(3;-1)

K là trung điểm của DD’ nên D’(3;-5)

$CD' = \sqrt {{5^2} + {6^2}}  = \sqrt {61}$

Vậy giá trị nhỏ nhất của $\left| {z + 2 - i} \right| + \left| {z - 3 - 3i} \right|$ là $\sqrt {61}$