Cho một tấm tôn hình vuông có cạnh bằng a. Người ta cắt 4 góc của tấm tôn để được một tấm tôn mới như hình vẽ.
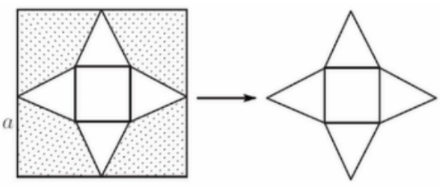
Từ tấm tôn mới, người ta gặp được một hình chóp tứ giác đều. Để khối chóp thu được có thể tích lớn nhất thì diện tích các miếng tôn bỏ đi là
Trả lời bởi giáo viên
Gọi x là độ dài của cạnh đáy của khối chóp
\(h\) là chiều cao của khối chóp, \(h'\) là chiều cao của tam giác cân ở mặt bên của khối chóp.
Bước 1: Biểu diễn h và thể tích V của khối chóp theo a và x
Ta có: \(x + 2h' = a\)\( \Rightarrow h' = \dfrac{{a - x}}{2}\)
Ta có: \({h^2} + {\left( {\dfrac{x}{2}} \right)^2} = {\left( {\dfrac{{a - x}}{2}} \right)^2}\) \( \Leftrightarrow h = \sqrt {{{\left( {\dfrac{{a - x}}{2}} \right)}^2} - {{\left( {\dfrac{x}{2}} \right)}^2}} = \dfrac{{\sqrt {{a^2} - 2ax} }}{2}\)
Thể tích khối chóp: \(V = \dfrac{1}{3}.\dfrac{{\sqrt {{a^2} - 2ax} }}{2}.{x^2}\)
\( = \dfrac{1}{6}\sqrt { - 2a{x^5} + {a^2}{x^4}} \)
Bước 2: Tìm max của \(f\left( x \right) = - 2a{x^5} + {a^2}{x^4}\) với x>0
Xét hàm số \(f\left( x \right) = - 2a{x^5} + {a^2}{x^4}\) với x>0
\({V_{\max }} \Leftrightarrow f{\left( x \right)_{\max }}\)
Ta có: \(f'\left( x \right) = - 10a{x^4} + 4{a^2}{x^3}\)
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{{2a}}{5}\end{array} \right.\)
\( \Rightarrow \max f\left( x \right) = f\left( {\dfrac{{2a}}{5}} \right) = \dfrac{{16{a^6}}}{{3125}}\)
Dấu “=” xảy ra khi và chỉ khi \(x = \dfrac{{2a}}{5}\)
Bước 3: Tìm phần diện tích bị bỏ
\( \Rightarrow\) Diện tích phần không bị bỏ là:
\(S = {x^2} + 4.\dfrac{1}{2}.x.\dfrac{{a - x}}{2} = \dfrac{{2{a^2}}}{5}\)
Diện tích bị bỏ là \(\dfrac{{3{a^2}}}{5}\)
Hướng dẫn giải:
Gọi x là độ dài của cạnh đáy của khối chóp
\(h\) là chiều cao của khối chóp, \(h'\) là chiều cao của tam giác cân ở mặt bên của khối chóp.
Bước 1: Biểu diễn h và thể tích V của khối chóp theo a và x
Bước 2: Tìm max của \(f\left( x \right) = - 2a{x^5} + {a^2}{x^4}\) với x>0
\({V_{\max }} \Leftrightarrow f{\left( x \right)_{\max }}\)
Bước 3: Tìm phần diện tích bị bỏ

