Trả lời bởi giáo viên
Đáp án đúng: b
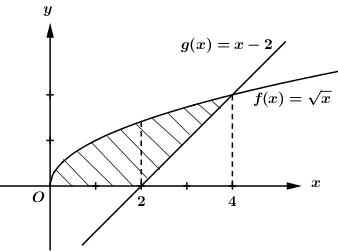
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(g\left( x \right) = x + 2;\,\,f\left( x \right) = \sqrt x \) là
\(\begin{array}{l}S = \int\limits_0^2 {\sqrt x dx} + \int\limits_2^4 {\left( {\sqrt x - x + 2} \right)dx} \\S = \left. {\dfrac{2}{3}x\sqrt x } \right|_0^2 + \left. {\left( {\dfrac{2}{3}x\sqrt x - \dfrac{{{x^2}}}{2} + 2x} \right)} \right|_2^4\\S = \dfrac{{4\sqrt 2 }}{3} + \dfrac{{16}}{3} - 2 - \dfrac{{4\sqrt 2 }}{3} = \dfrac{{10}}{3}\end{array}\)
Hướng dẫn giải:
Áp dụng công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Câu hỏi khác
- Bài tập nguyên hàm toán 12 có lời giải
- Bài tập tích phân các hàm số cơ bản toán 12 có lời giải
- Bài tập tích phân có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp từng phần để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp đổi biến để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
