Câu hỏi:
2 năm trước
Tính diện tích hình thang ABCD có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, BD = 15cm.
Trả lời bởi giáo viên
Đáp án đúng: a
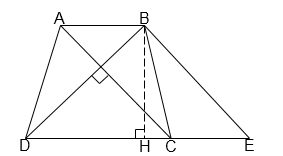
Qua B vẽ đường thẳng song song với \(AC\) , cắt \(DC\) ở \(E\) . Gọi \(BH\) là đường cao của hình thang. Ta có \(BE//AC,AC \bot BD\) nên \(BE \bot BD\)
Áp dụng định lý Pitago vào tam giác vuông \(BDH\) , ta có: \(B{H^2} + H{D^2} = B{D^2}\)
\( \Rightarrow {12^2} + H{D^2} = {15^2} \Rightarrow H{D^2} = 81 \Rightarrow HD = 9cm\)
Xét tam giác \(BDE\) vuông tại \(B\):
\(B{D^2} = DE.DH \Rightarrow {15^2} = DE.9 \Rightarrow DE = 25(cm)\)
Ta có: \(AB = CE\) nên \(AB + CD = CE + CD = DE = 25cm\)
Do đó: \({S_{ABCD}} = 25.12:2 = 150(c{m^2})\)
Hướng dẫn giải:
Sử dụng định lý Pytago tính \(HD\)
Sử dụng hệ thức lượng trong tam giác vuông tính \(DE.\)
Diện tích hình thang bằng tích của tổng hai đáy với chiều cao chia 2.
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
