Trả lời bởi giáo viên
Đáp án đúng: c
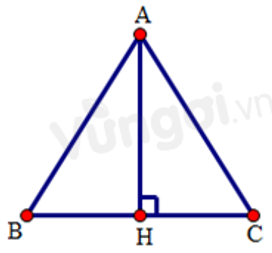
Sử dụng kết quả câu trước ta có \(BH = 3\,cm.\)
\(\Delta ABC\) cân tại \(A\) nên \(AB = AC = 5\,cm.\)
Áp dụng định lý Pytago vào tam giác \(ACH\)vuông tại \(H\) ta có:
\(A{C^2} = C{H^2} + A{H^2} \Rightarrow C{H^2} = A{C^2} - A{H^2}\)
\( \Rightarrow C{H^2} = {5^2} - {4^2} = 9 \Rightarrow CH = \sqrt 9 \, = 3\,\left( {cm} \right).\)
Suy ra \(BC = BH + CH = 3 + 3 = 6\,cm.\)
Vậy chu vi tam giác \(ABC\) là: \(AB + AC + BC = 5 + 5 + 6 = 16\,\left( {cm} \right)\).
Hướng dẫn giải:
- Áp dụng định lý Pytago: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
- Áp dụng tính chất: Tam giác cân có hai cạnh bên bằng nhau.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
