Câu hỏi:
2 năm trước
Tìm tất cả các giá trị thực của $m$ để phương trình \(2{\log _2}\left| x \right| + {\log _2}\left| {x + 3} \right| = m\) có $3$ nghiệm thực phân biệt.
Trả lời bởi giáo viên
Đáp án đúng: d
TXĐ : \(D = R\).
\(2{\log _2}\left| x \right| + {\log _2}\left| {x + 3} \right| = m \Leftrightarrow {\log _2}{\left| x \right|^2} + {\log _2}\left| {x + 3} \right| = m \)
$\Leftrightarrow {\log _2}\left( {{{\left| x \right|}^2}.\left| {x + 3} \right|} \right) = m \Leftrightarrow {\left| x \right|^2}.\left| {x + 3} \right| = {2^m}$
\( \Leftrightarrow {x^2}.\left| {x + 3} \right| = {2^m}\).
Xét hàm \(f(x) = {x^2}.\left| {x + 3} \right|\). Ta có : \(f(x) = {x^2}.\left| {x + 3} \right| = \left| {{x^3} + 3{x^2}} \right|\)
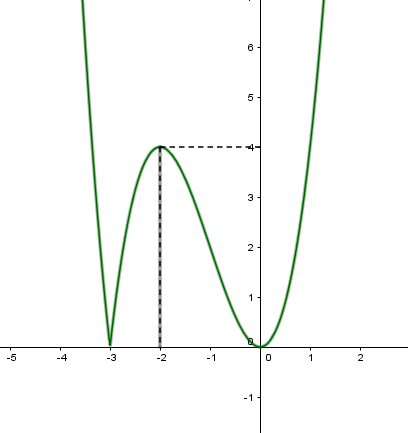
Để phương trình có 3 nghiệm phân biệt thì \({2^m} = 4 \Leftrightarrow m = 2\)
Hướng dẫn giải:
\({\log _a}f(x) = b \Leftrightarrow f(x) = {a^b}\)
