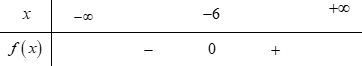Câu hỏi:
2 năm trước
Tìm $m$ để $\left( {m + 1} \right){x^2} + mx + m < 0,\forall x \in \mathbb{R}$?
Trả lời bởi giáo viên
Đáp án đúng: c
Với \(m = - 1\) thì bpt trở thành \( - x - 1 < 0 \Leftrightarrow x > - 1\) nên bpt không đúng với mọi x (loại)
Do đó m=-1 không thỏa mãn.
Với \(m \ne - 1\), $\left( {m + 1} \right){x^2} + mx + m < 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right.$\( \Leftrightarrow \left\{ \begin{array}{l}m + 1 < 0\\{m^2} - 4m\left( {m + 1} \right) < 0\end{array} \right.\)
$ \Leftrightarrow \left\{ \begin{array}{l}m + 1 < 0\\ - 3{m^2} - 4m < 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}m < - 1\\\left[ \begin{array}{l}m < - \dfrac{4}{3}\,\\m > 0\end{array} \right.\end{array} \right.$$ \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
m < - 1\\
m < - \frac{4}{3}
\end{array} \right.\\
\left\{ \begin{array}{l}
m < - 1\\
m > 0
\end{array} \right.\left( {VN} \right)
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m < - 1\\
m < - \frac{4}{3}
\end{array} \right.$ $ \Leftrightarrow m < - \dfrac{4}{3}$.
Hướng dẫn giải:
Tam thức bậc hai \(f\left( x \right) < 0,\forall x \in R \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right.\)
