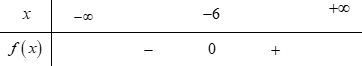Câu hỏi:
2 năm trước
Bảng xét dấu nào sau đây là của tam thức $f\left( x \right) = \;{x^2} + 12x + 36$?
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
$\begin{array}{l}
f\left( x \right) = {x^2} + 12x + 36\\
\Delta = {12^2} - 4.1.36 = 0
\end{array}$
Do đó, tam thức bậc hai \(f(x) \) có một nghiệm duy nhất \(x = - \frac{{12}}{{2.1}} = - 6\)
\(a = 1 > 0\) nên \(f\left( x \right) > 0,\forall x\ne -6\) hay \(f(x)\ge 0\) với mọi x.
Do đó ta có bảng xét dấu cần tìm.
Hướng dẫn giải:
Tìm nghiệm của \(f\left( x \right)\), nhận xét hệ số \(a\) và đối chiếu đáp án.
Giải thích thêm:
Cách trình bày phía trên là dựa vào định lý dấu của tam thức bậc hai trong trường hợp \(\Delta =0\) thì \(f(x)\) cùng dấu với a với mọi x khác -b/2a.
Thực tế bài này chỉ cần làm như sau:
$\begin{array}{l}
f\left( x \right) = {x^2} + 12x + 26\\
= {x^2} + 2.6.x + {6^2} = {\left( {x + 6} \right)^2} \ge 0,\forall x
\end{array}$
Từ đó có ngay bảng xét dấu.
